Représentations graphiques avec ggplot2

De la théorie à la pratique sur les microdonnées de l’enquête Étude des Relations Familiales et Intergénérationnelles (ERFI)

Auteur·rice·s

Affiliations

Maude Crouzet

PUD de Strasbourg (PUD-S), MISHA

Claire Kersuzan

PUD de Bordeaux (PUD-Bx), MSH-Bx, Université de Bordeaux

Présentation et organisation de la formation

Introduction

La visualisation des données est un élément clé de l’analyse et de la communication scientifique. Elle permet de rendre compréhensibles des ensembles de données complexes ou volumineux, souvent difficiles à appréhender via des tableaux ou des textes denses. Des graphiques clairs et efficaces augmentent l’impact des travaux scientifiques, favorisant leur partage et leur citation (Jensen et al., 2023; Lee et al., 2016; Murray et al., 2017). Lors des conférences, ils constituent également un outil essentiel pour présenter des résultats de manière visuelle et accessible. Enfin, ils renforcent la transparence et la reproductibilité des recherches, contribuant à diffuser les connaissances et à encourager les collaborations dans le cadre de la science ouverte¹. 

Pour créer des graphiques percutants, il est nécessaire de suivre des principes adaptés au type de données et aux objectifs de communication, notamment en utilisant des types de graphique, des couleurs, des formes et des agencements appropriés. Le package ggplot2, basé sur la “Grammaire des graphiques”, est un outil incontournable pour produire des visualisations scientifiques esthétiques, reproductibles et hautement personnalisables. Il offre une flexibilité permettant de concevoir des graphiques clairs et rigoureux, parfaitement alignés avec les exigences de la science ouverte.

Cette formation poursuit trois objectifs principaux :

1. Maîtriser les principes fondamentaux de la représentation graphique afin de créer des visualisations claires et informatives, en tenant compte du type de variables à représenter (quantitatives ou qualitatives), des bonnes pratiques de sémiologie graphique (couleurs, formes, tailles, dispositions) et en intégrant des éléments essentiels tels que la légende, la source, le titre, ainsi que le choix des axes et des échelles.
2. Apprendre à utiliser le package R ggplot2, une extension du tidyverse et un outil puissant pour concevoir des graphiques reproductibles et esthétiques à partir d’une synthaxe cohérente et unifiée.
3. Illustrer l’enseignement et mettre en pratique les compétences acquises à l’aide de microdonnées issues d’une enquête réelle, l’enquête “Étude des relations familiales et intergénérationnelles” (ERFI-1), réalisée en 2005 par l’INED (Institut National des Études Démographiques) et l’INSEE (Institut National de la Statistique et des Études Économiques). L’exercice proposé consiste à reproduire certains graphiques d’un article scientifique d’Arnaud Régnier-Loilier, publié en 2006 dans la revue Population et Sociétés : “À quelle fréquence voit-on ses parents ?”. Cet exercice vise également à encourager l’utilisation des données issues du nouveau cycle d’enquêtes ERFI-2, dont la collecte, lancée en 2023, s’inscrit dans le cadre du projet LifeObs coordonné par l’INED. La disponibilité prochaine des données d’ERFI-2 via l’application Quetelet Progedo-Diffusion ouvre de nombreuses perspectives pour analyser les comportements familiaux récents et leurs évolutions depuis le premier cycle d’enquêtes ERFI-1.

L’enquête Etude des relations familiales et intergénérationnelles (ERFI)

L’enquête Étude des relations familiales et intergénérationnelles (ERFI) est la branche française du programme européen Generations and Gender Programme (GGP). Mis en place en 2000 à l’initiative de la Population Activities Unit de la Commission économique des Nations Unies pour l’Europe, ce programme vise à collecter des informations afin d’éclairer les évolutions récentes du paysage sociodémographique : vieillissement de la population, baisse de la fécondité, fragilisation des unions, féminisation du marché du travail et les enjeux que soulèvent ces transformations (solidarités intergénérationnelles, redéfinition des rôles des hommes et des femmes dans la société ou au sein des couples).

Des données ont été collectées selon une méthodologie similaire dans 24 pays (principalement en Europe), avec un questionnaire standardisé permettant une comparaison internationale. L’ensemble des thématiques abordées ainsi que les questionnaires des enquêtes peuvent être consultés sur le site de l’enquête ERFI-1.
Il s’agit d’un panel, c’est-à-dire d’une enquête qui réinterroge les mêmes individus à plusieurs intervalles de temps (trois vagues en France : 2005, 2008 et 2011). La première enquête, ERFI-1, a été menée en face-à-face auprès de 10 079 personnes âgées de 18 à 79 ans vivant en France métropolitaine. Elle permet ainsi de mesurer l’évolution des situations ou encore les décalages entre intentions et réalisations.

Le programme GGP a été relancé en 2020 avec un nouveau cycle d’enquêtes, reposant sur un panel distinct mais un questionnaire très proche de celui du premier cycle. En France, la première vague d’ERFI-2 a été lancée en 2023. Contrairement à ERFI-1, cette nouvelle enquête est réalisée par téléphone, et non en face-à-face.

Pré-requis

Il est recommandé d’avoir une connaissance de base du langage R et de son interface RStudio, incluant la manipulation d’objets, de variables et de données à l’aide des packages du tidyverse, ainsi que le calcul de statistiques simples (notamment de proportions). Ces compétences peuvent être acquises en suivant le kit pédagogique Initiation à l’exploitation de données d’enquête avec le langage R - ERFI-1.

Déroulé de la formation (ou auto-formation)

La formation (ou auto-formation), d’une durée de 6 heures, s’adresse aux chercheur·e·s, étudiant·e·s, doctorant·e·s et personnels de soutien à la recherche souhaitant acquérir des compétences de base en représentation graphique avec ggplot2.
Elle comprend une introduction théorique aux principes fondamentaux de la visualisation des données, une présentation des concepts clés de ggplot2, ainsi qu’une application pratique consistant à reproduire certains graphiques tirés d’un article scientifique, en utilisant un fichier de production anonymisé à visée pédagogique (FPA) de l’enquête ERFI-1 fourni par le Service des Enquêtes de l’INED.

Exercice pratique

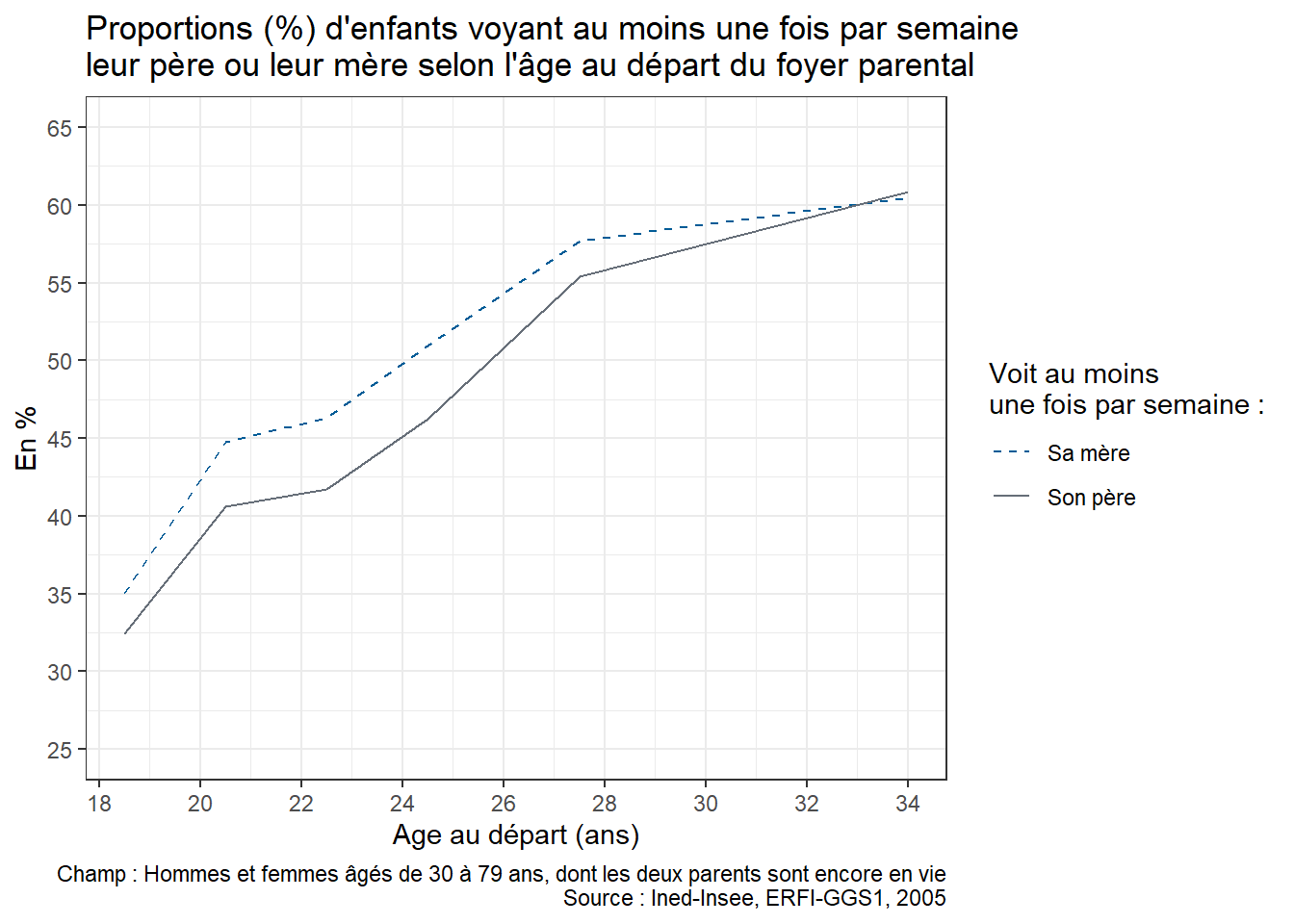
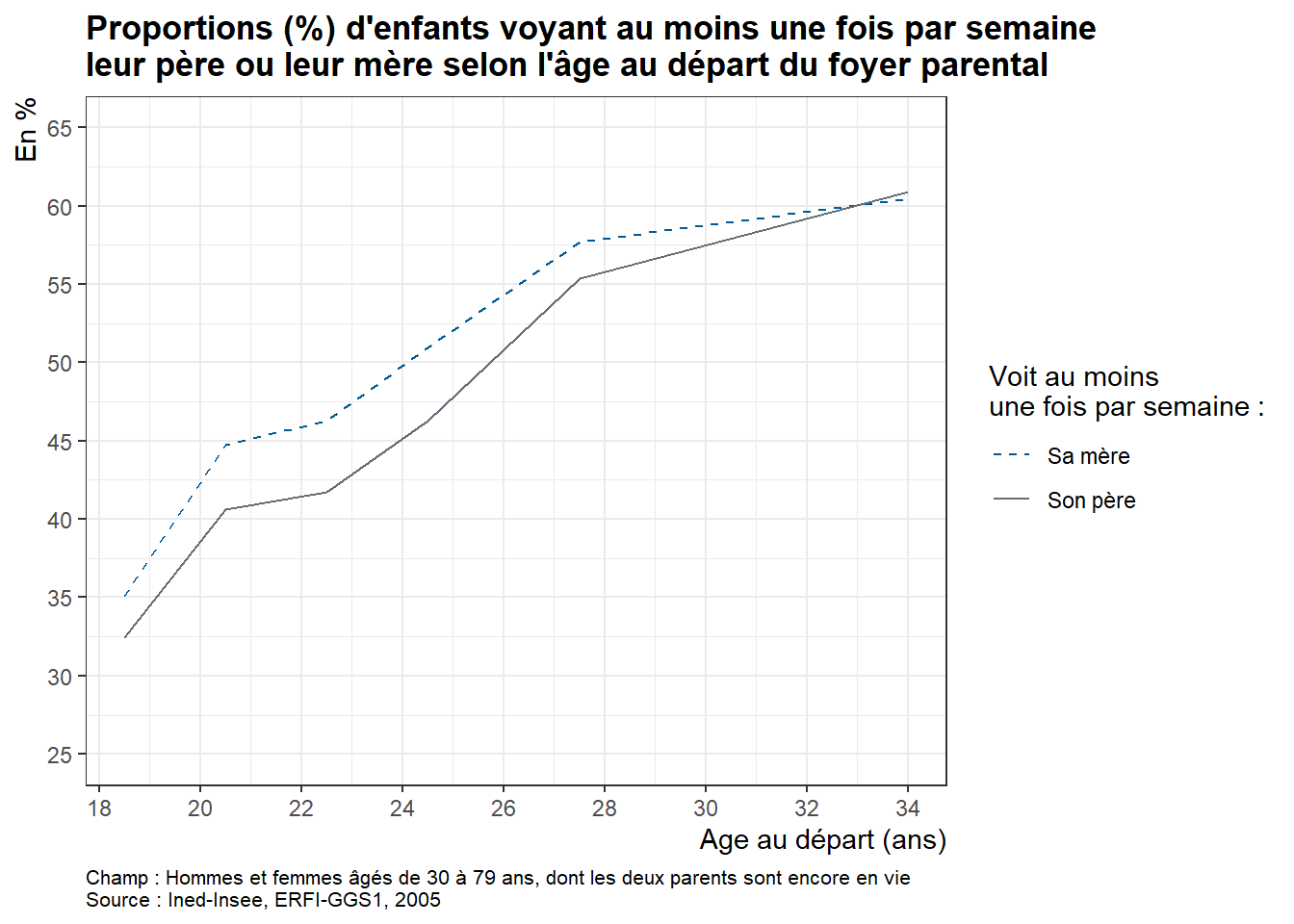
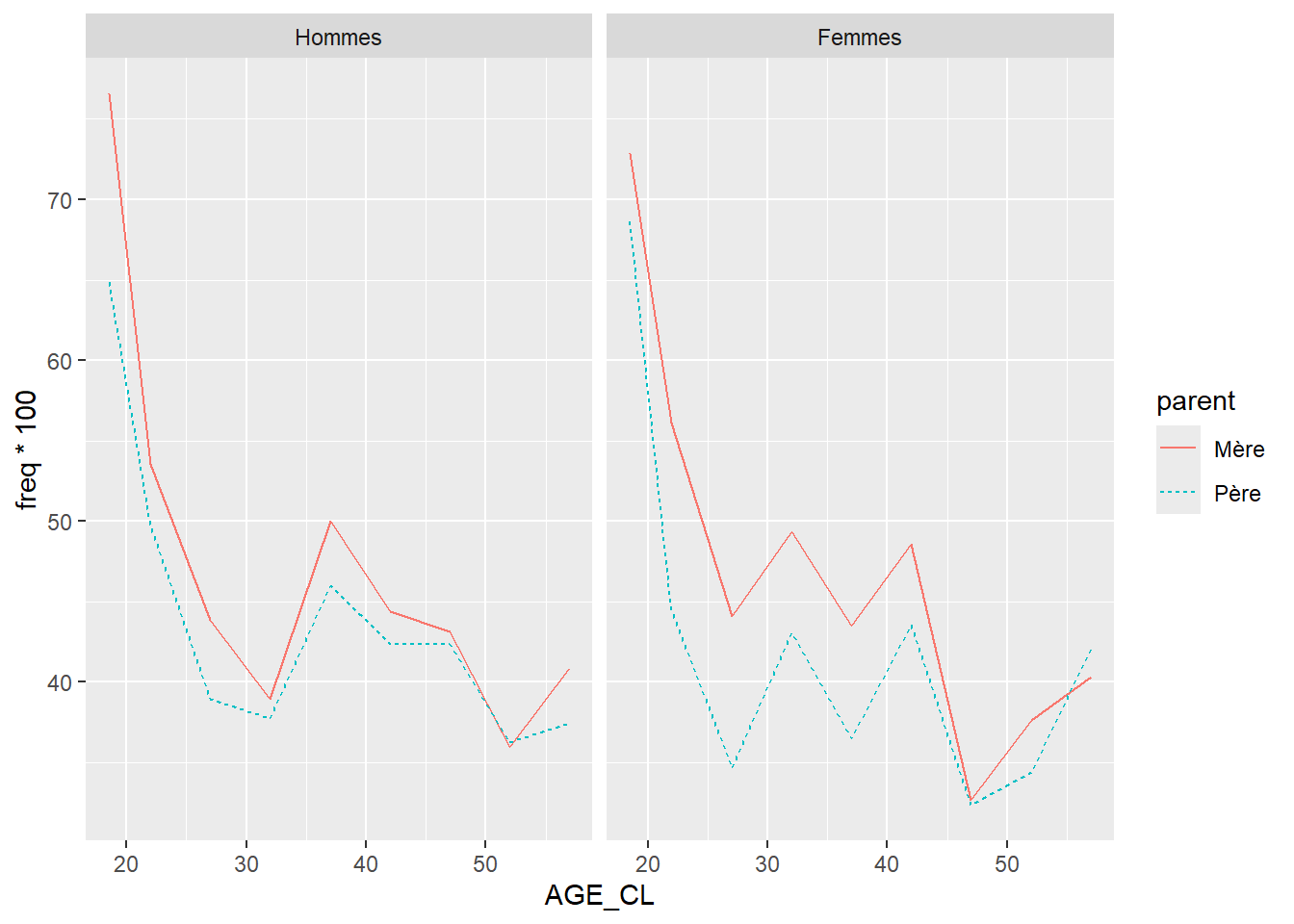
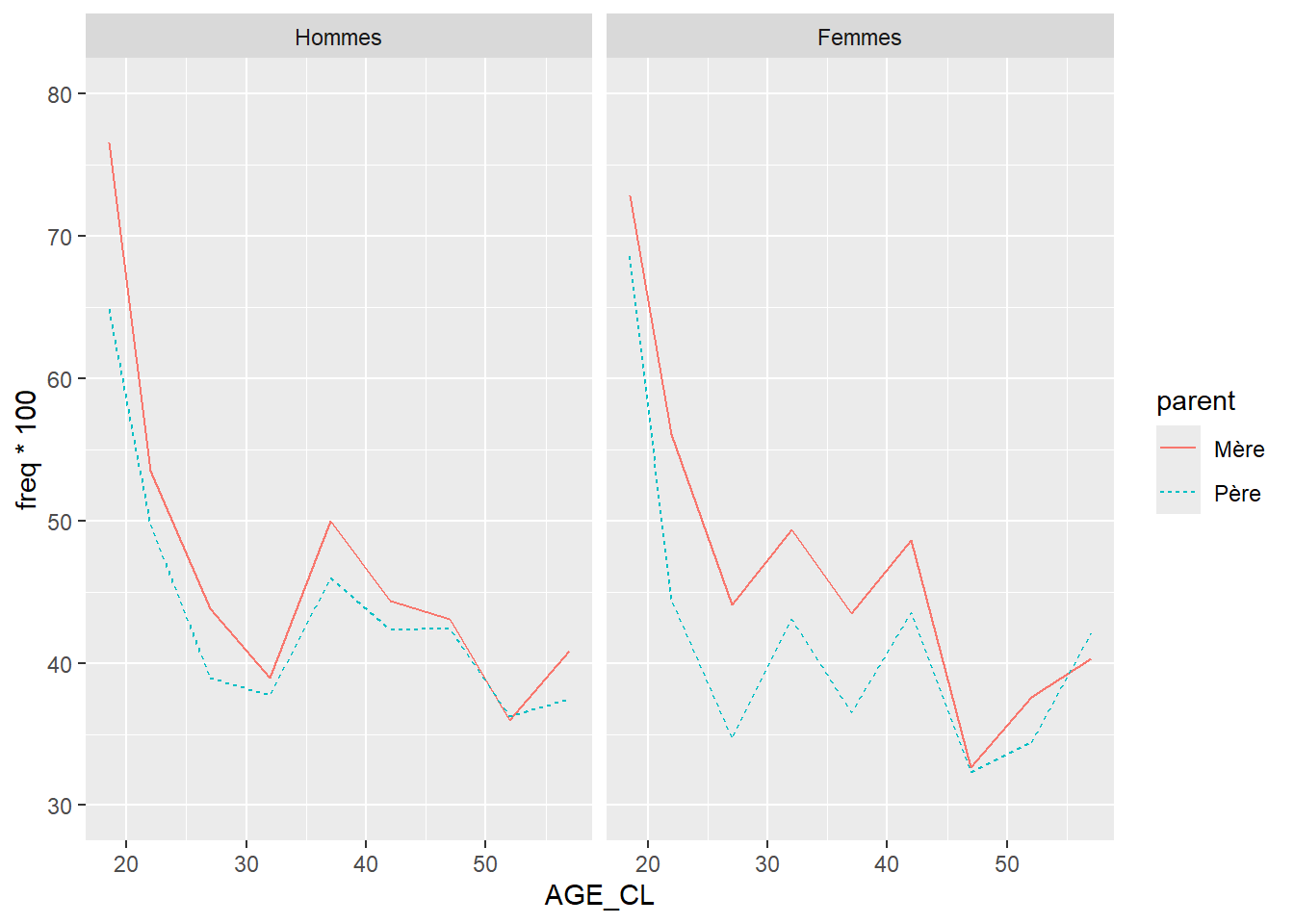
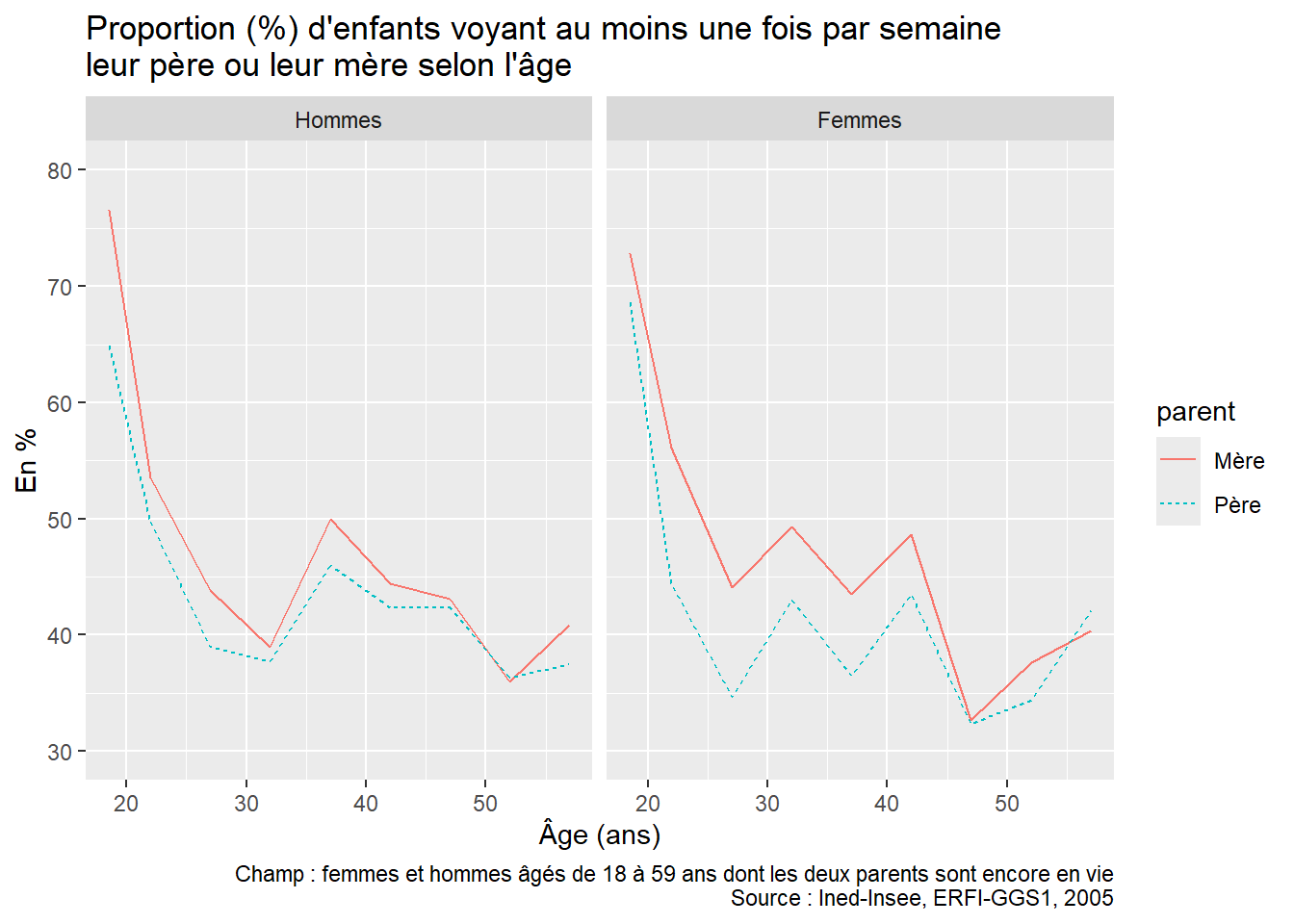
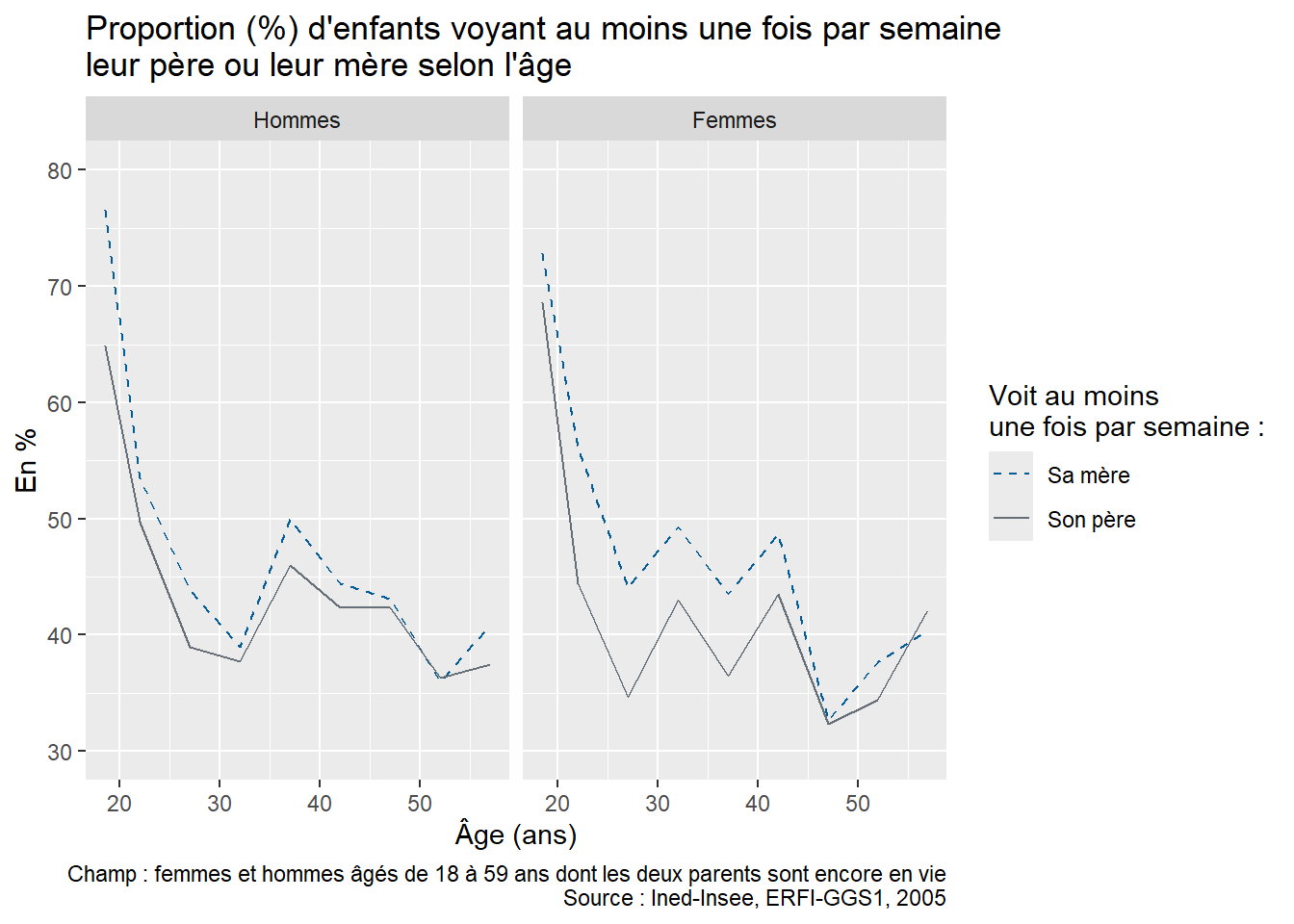
Pour permettre aux apprenant·e·s de s’exercer par eux-mêmes, il est possible de proposer en fin de séance la reproduction de la figure 2 « Proportion (%) d’enfants qui voient leurs parents au moins une fois par semaine selon la configuration familiale durant l’enfance » de l’article utilisé pour la formation “À quelle fréquence voit-on ses parents ?” (Arnaud Régnier-Loilier, 2006). Pour cette reproduction, on utilisera sur l’axe des abscisses les catégories suivantes : “Avec ses parents”, “Avec sa mère seule”, “Avec son père seul”, “Avec un parent et un beau-parent”, “Avec un/des grand(s)-parent(s)”, “Autres situations”.

Fichier de production anonymisé à visée pédagogique (FPA)

L’anonymisation est une procédure qui vise à supprimer tout caractère identifiant, direct (nom, adresse, numéro de sécurité sociale, etc.) ou indirect (issu du croisement de plusieurs variables comme par exemple l’âge, la PCS et le nombre d’enfants), d’un fichier de données individuelles (ou microdonnées).

L’application de cette procédure peut induire des suppressions ou des modifications dans les données collectées : suppression locale d’informations, modification de valeurs, échanges de valeurs entre individus, etc. La conséquence est que les résultats tirés d’un tel fichier ne peuvent pas être utilisés à des fins scientifiques.
Les microdonnées anonymisées mises à disposition sous forme de fichiers de production anonymisés à visée pédagogique (FPA) relèvent de l’open data : elles sont en accès libre et gratuit, mais uniquement à des fins pédagogiques.

En revanche, le FPA utilisé dans cette formation (ou auto-formation) permet de reproduire des résultats proches des tableaux et figures de l’article publié dans Population et Sociétés qui sert de support ici. Il ne permet pas de réaliser l’ensemble des traitements possibles sur les données complètes, mais constitue une ressource adaptée à un usage strictement pédagogique.

Des détails concernant les procédures d’anonymisation appliquées par le Service des enquêtes de l’INED au FPA de l’enquête ERFI-1 sont accessibles ici.

Documents de la formation (ou auto-formation)

Cette formation s’appuie sur l’utilisation de plusieurs ressources :

• un fichier de production anonymisé à visée pédagogique (FPA) de l’enquête ERFI-1 préparé par le Service des Enquêtes de l’INED - SES (Institut national d’études démographiques). Il contient une sélection des réponses originales de l’enquête ERFI-1 dont certaines sont recodées/modifiées en vue de leur anonymisation.
• ce support de formation (conçu sous RStudio avec Quarto) mêlant exposés théoriques (grands principes de la représentation graphique, présentation du package ggplot2) et un cas pratique détaillant les différentes opérations à réaliser (instructions R et résultats de leur exécution) permettant de reproduire les premiers graphiques d’un article écrit par Arnaud Régnier-Loilier en 2006 dans la revue Population et Sociétés: “À quelle fréquence voit-on ses parents?”.
• d’autres documents utiles à la formation : documentations du jeu de données anonymisé et des données de l’enquête originale ERFI-1, article de la revue Population et Sociétés dont certains résultats sont ici répliqués, dictionnaire des variables du fichier anonymisé ERFI-1, etc.

1. Les grands principes de la représentation graphique

1.1 Rôle de la représentation graphique dans l’analyse de données

La représentation graphique est un outil fondamental dans l’analyse de données. Elle intervient à plusieurs niveaux, depuis l’exploration des données jusqu’à la communication des résultats.

Pour l’analyse exploratoire

Les graphiques exploratoires permettent de mieux comprendre la structure du jeu de données : dimensions, distributions des variables, valeurs manquantes ou aberrantes, fréquences des modalités d’une variable catégorielle, et relations entre variables.

Par exemple, ils aident à :
- repérer des valeurs atypiques ou des anomalies,
- visualiser la répartition d’une variable quantitative,
- identifier des tendances ou corrélations entre variables.

Ces informations servent à orienter les choix de traitements ou de transformations des données (nettoyage, regroupement de modalités, normalisation, codage de variables, etc.) et à sélectionner les méthodes statistiques adaptées.

Les graphiques exploratoires sont principalement destinés à l’équipe de recherche. Ils n’ont pas vocation à être publiés et n’ont pas besoin d’être esthétiquement parfaits. Au contraire, il est souvent utile de générer rapidement plusieurs graphiques pour examiner différents aspects du jeu de données.

Sur R, le package DataExplorer permet de réaliser rapidement un grand nombre de graphiques exploratoires. Un article présentant ses principales fonctions est disponible ici.

Pour la mise en œuvre d’analyses statistiques

Les graphiques sont également utiles pour vérifier et interpréter les résultats d’analyses statistiques : analyse factorielle, modèles de régression, ANOVA, etc. Ils permettent de détecter des écarts par rapport aux hypothèses des modèles, de visualiser les effets ou relations significatives, et de guider l’interprétation des résultats. Les logiciels statistiques génèrent souvent ces graphiques automatiquement comme partie intégrante des sorties.

Pour la communication et la valorisation des résultats

Enfin, les graphiques jouent un rôle central dans la diffusion et la valorisation des résultats. Contrairement aux graphiques exploratoires, leur objectif est de transmettre une information clé à un public ciblé.

Dans un article, un rapport ou une présentation, un graphique bien conçu :
- attire davantage l’attention qu’un tableau,
- facilite la compréhension des résultats, même pour un public peu habitué aux données quantitatives.

Il est donc essentiel de sélectionner les informations les plus pertinentes, d’accorder une attention aux aspects esthétiques, et d’accompagner le graphique d’éléments informatifs (titre, source, champ, note de lecture) pour assurer une lecture correcte et efficace.

1.2 Choisir le bon type de représentation graphique selon la nature des variables

Le choix du graphique à réaliser dépend du nombre et de la nature des variables que l’on souhaite représenter.

Rappel sur les types de variables

• Variable quantitative : décrit un caractère quantifiable sur lequel il est possible de réaliser des opérations arithmétiques (calcul de la moyenne par exemple)
  • Continue : prend un nombre infini de valeurs au sein d’un intervalle donné (ex : âge)
  • Discrète : peut prendre un nombre fini de valeurs au sein d’un intervalle donné (ex : nombre d’enfants)
• Variable qualitative (aussi appellée variable catégorielle) : décrit un caractère qui n’est pas quantifiable.
  • Nominale : les modalités de la variable n’ont pas d’ordre naturel ou logique. Autrement dit, changer l’ordre dans lequel sont présentées les modalités n’affecte pas la compréhension de l’information présentée (ex : statut matrimonial)
  • Ordinale : les modalités de la variables ont un ordre naturel ou logique (ex : niveau de diplôme)

Représenter une seule variable

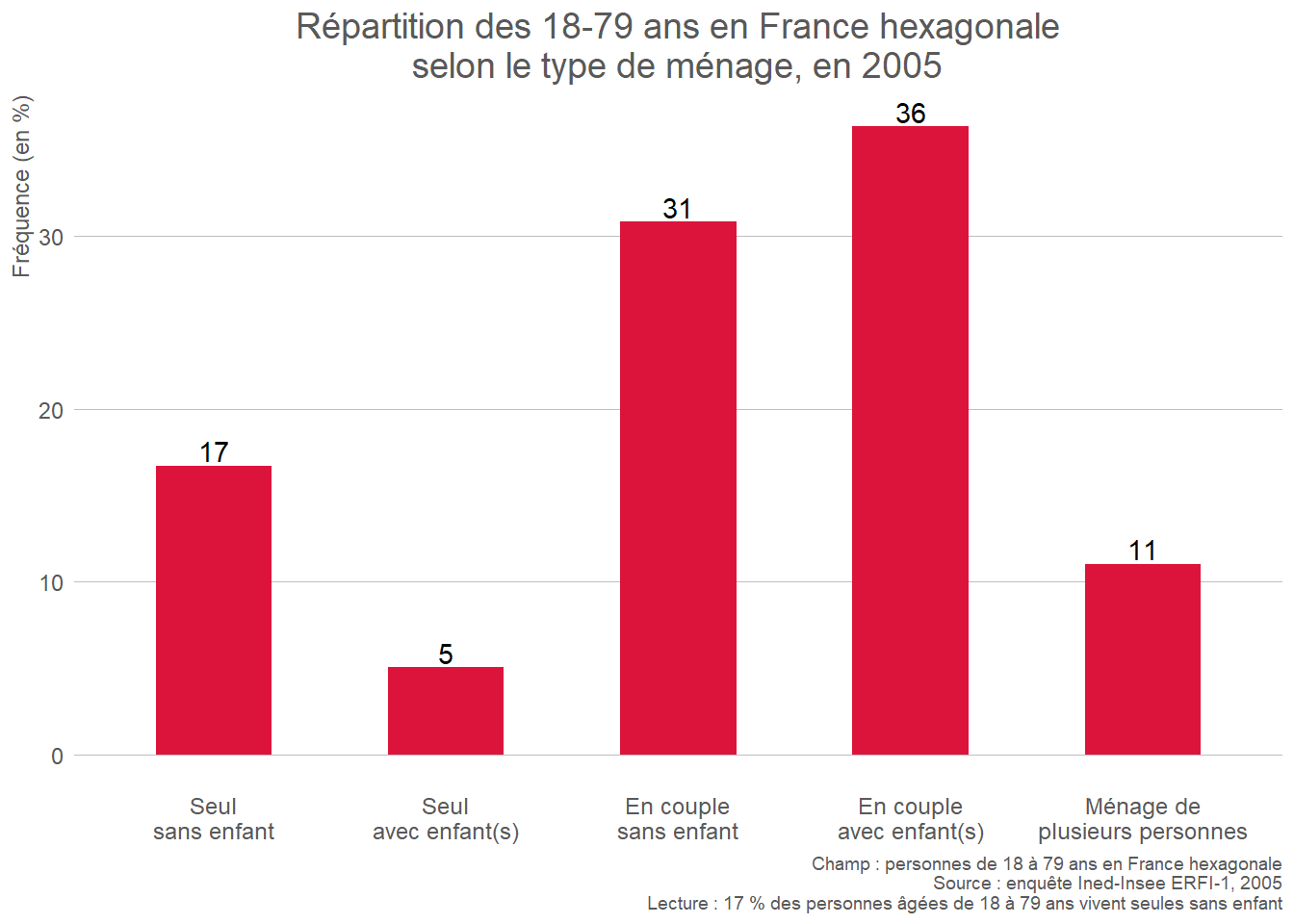
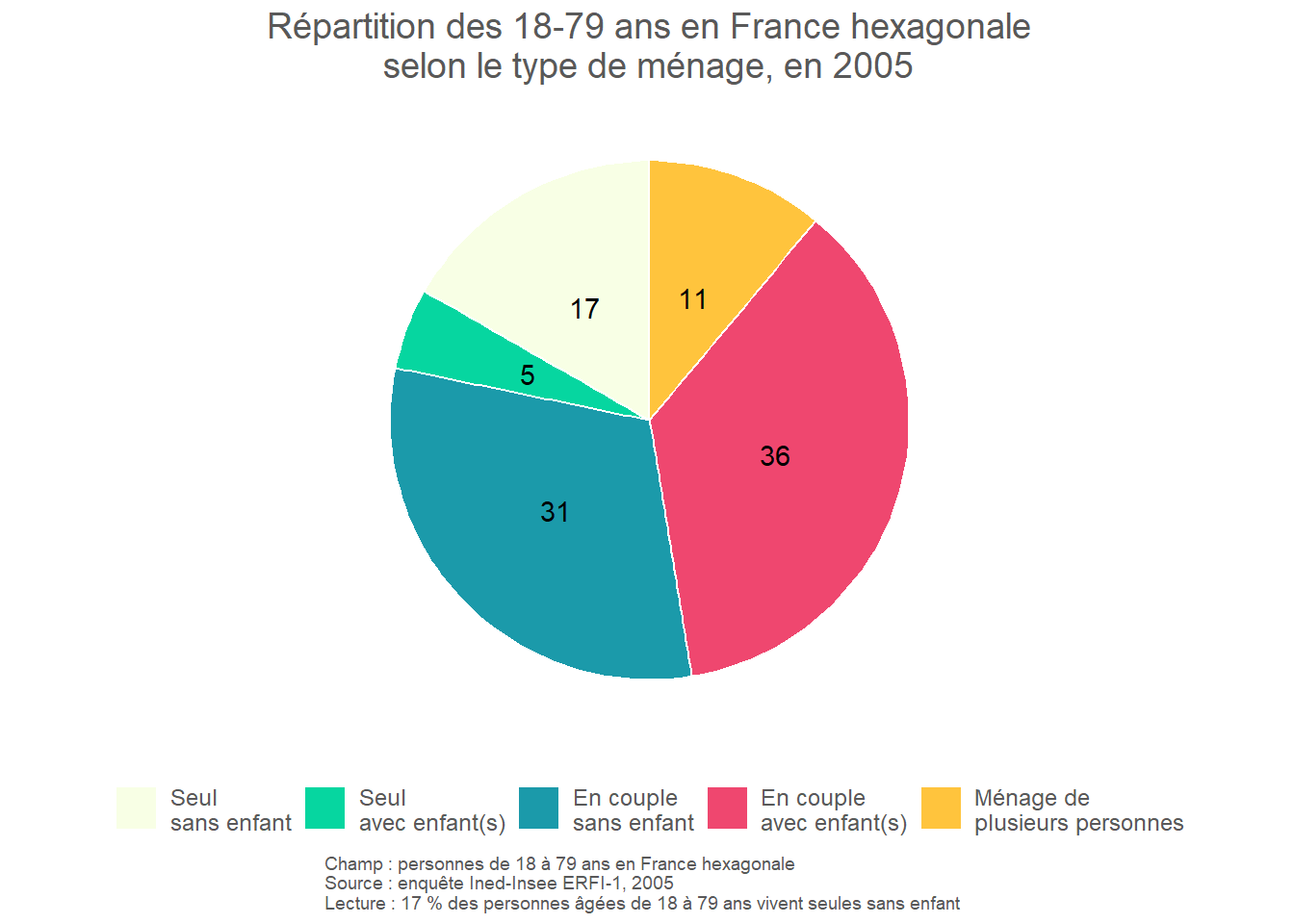
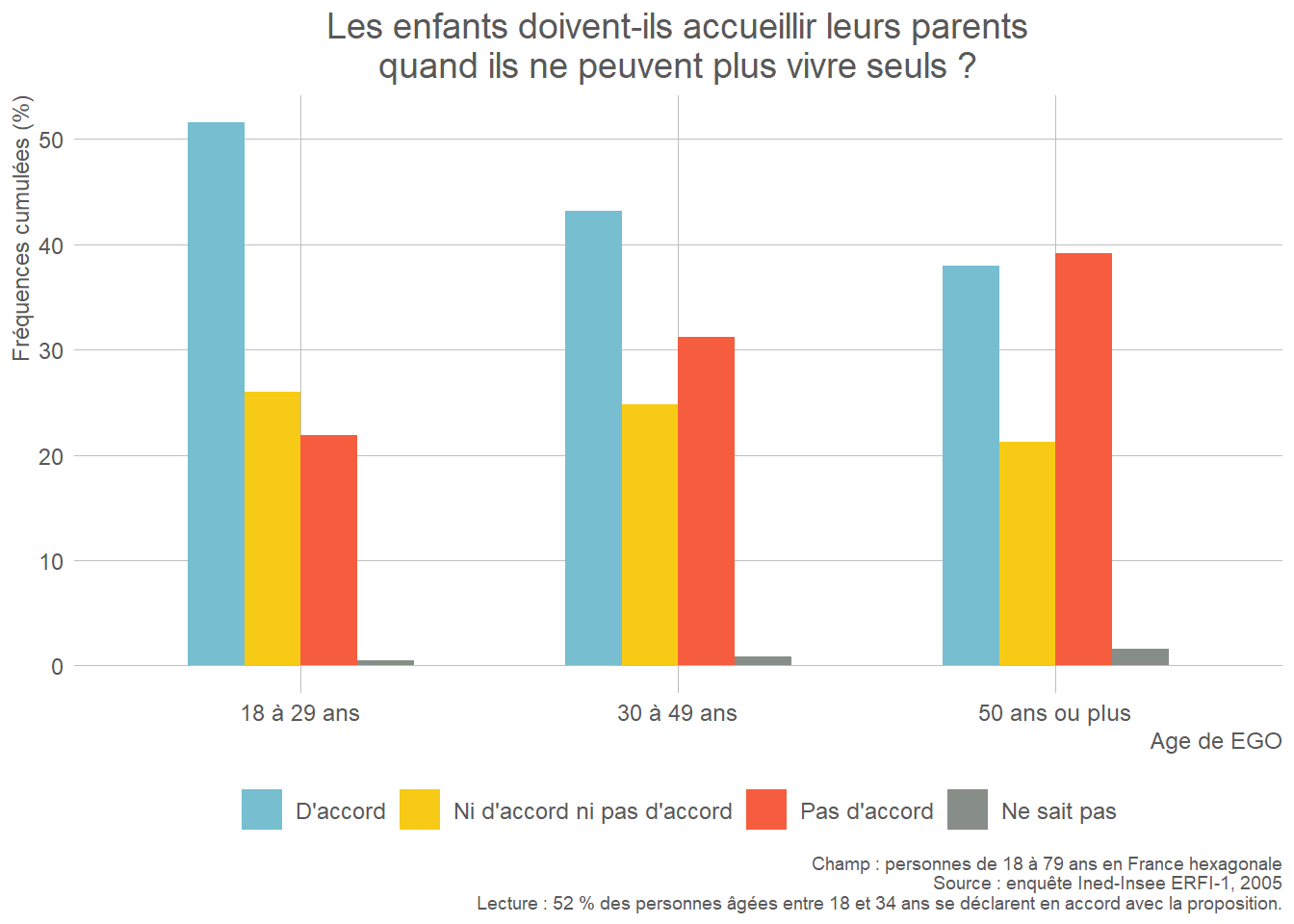
• Qualitative : diagramme en barres (barplot) ou diagramme circulaire (pie chart).
  Le diagramme en barres est à privilégier pour les variables qualitatives ordinales, car il permet de visualiser facilement la distribution de la population selon la hiérarchie des modalités. Le diagramme circulaire (communément appelé “camembert”) est adapté aux variables qualitatives nominales comportant au plus 4 modalités. Au-delà, il devient plus difficile à lire, particulièrement si certaines modalités sont peu représentées. Le diagramme en barres se prête mieux aux variables comportant un grand nombre de modalités.

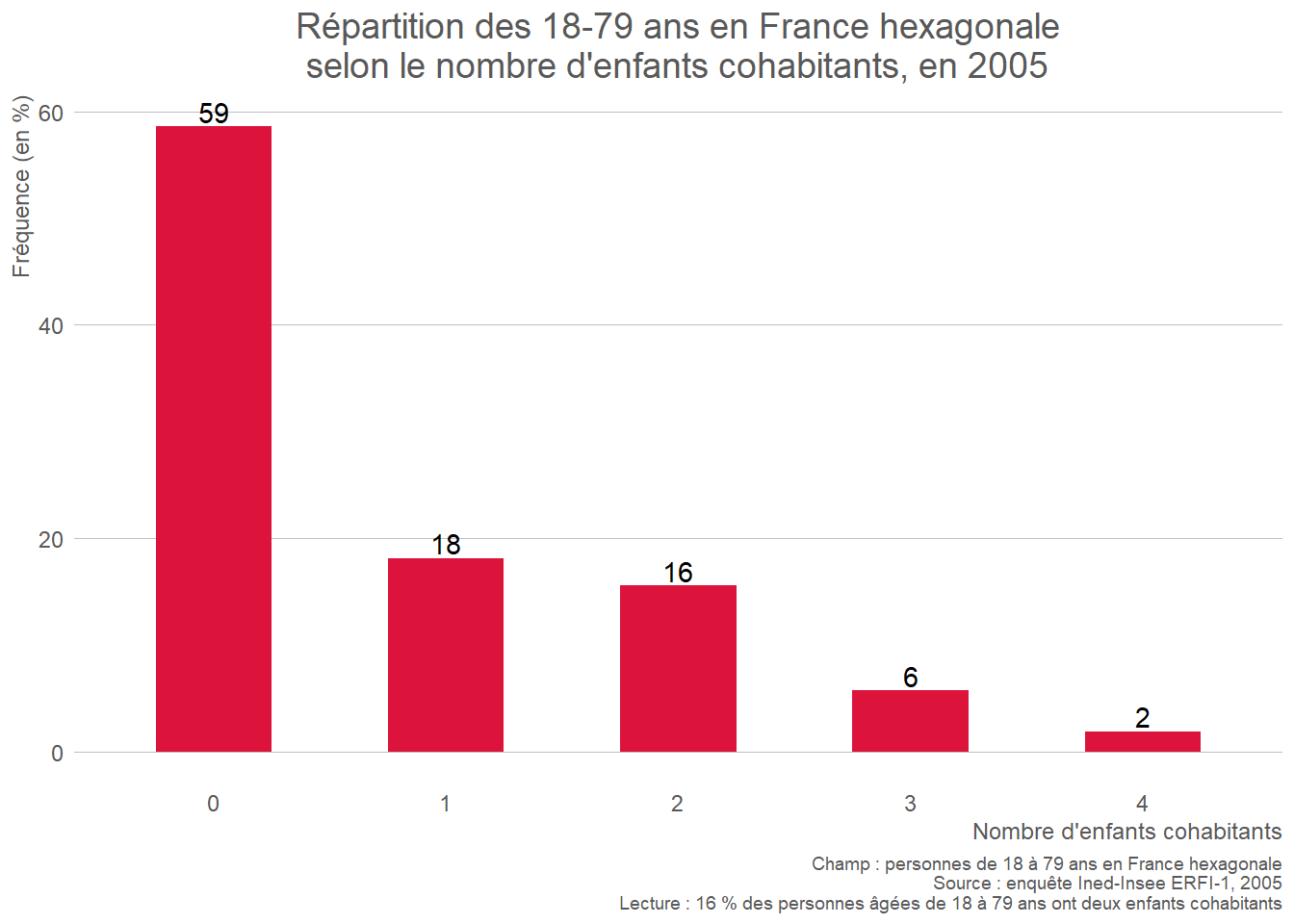
• Quantitative discrète : diagramme en barres.

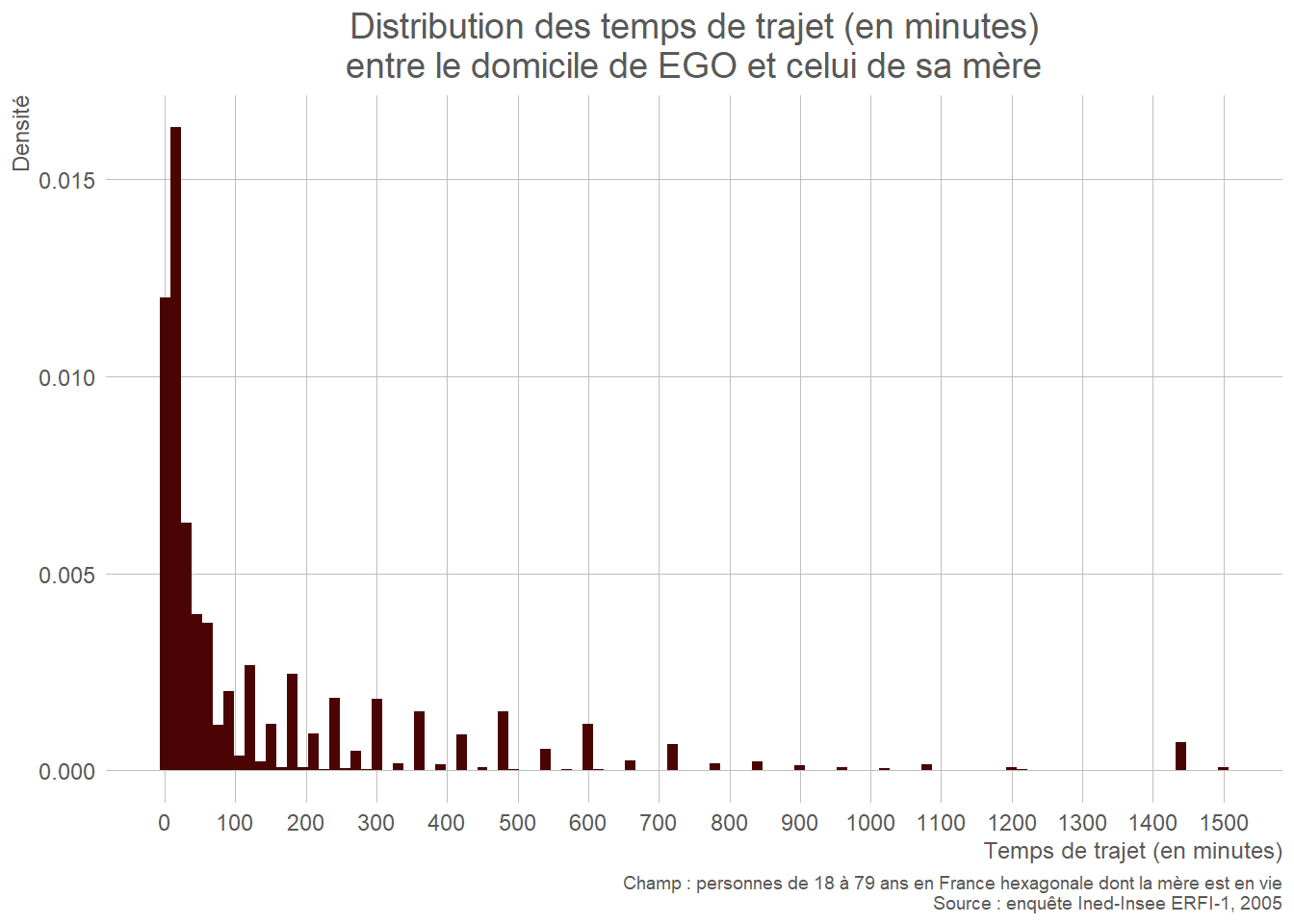
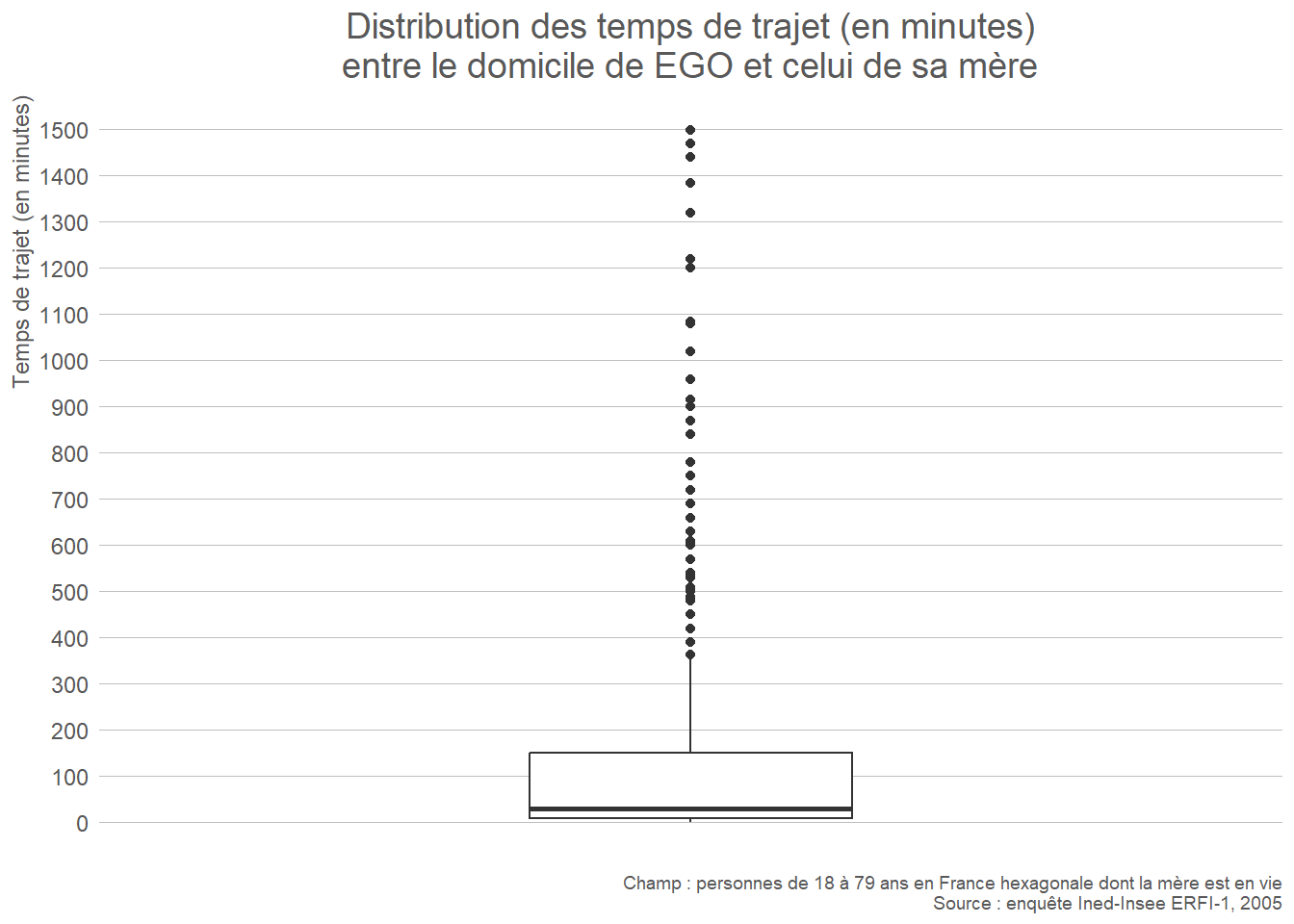
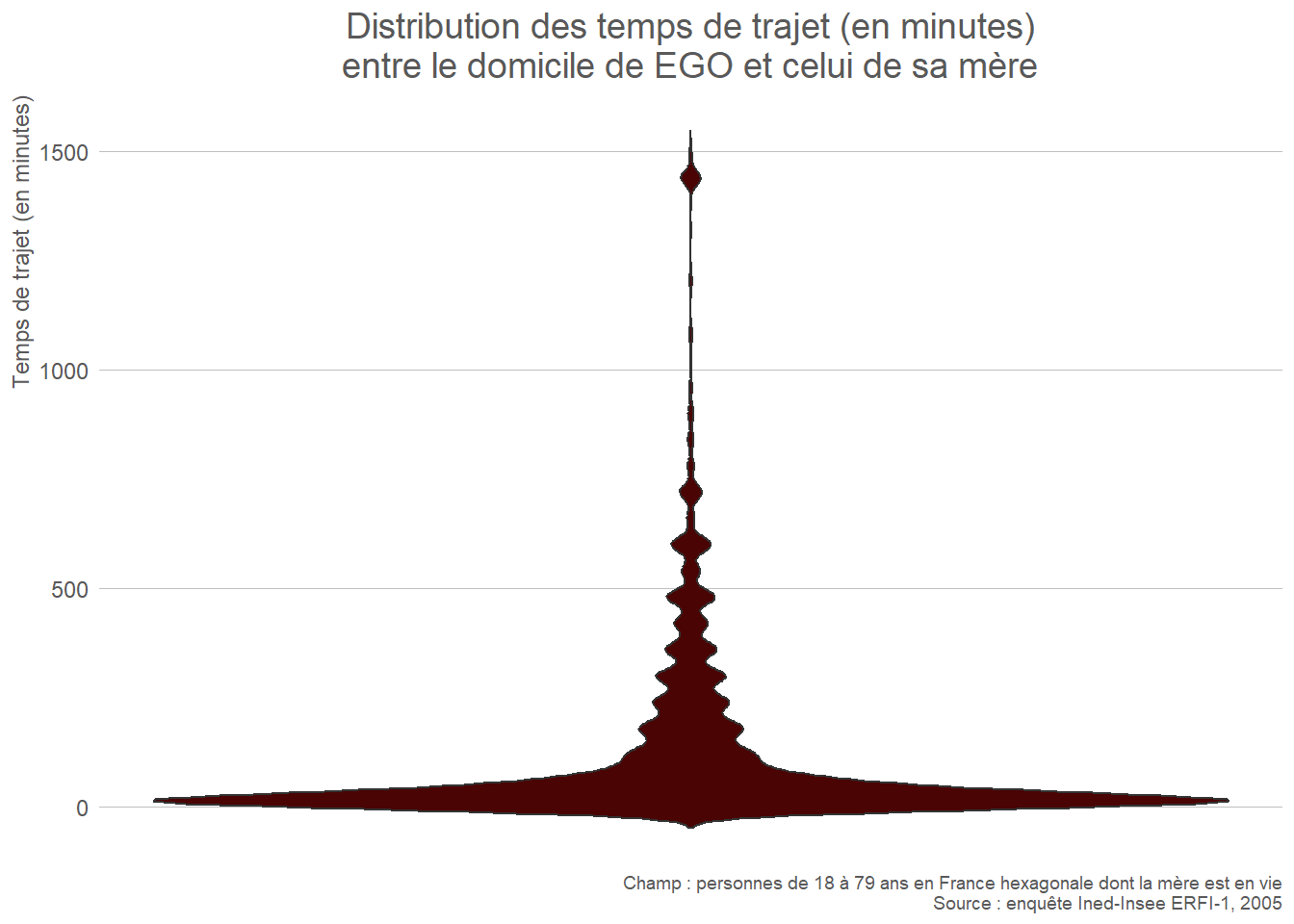
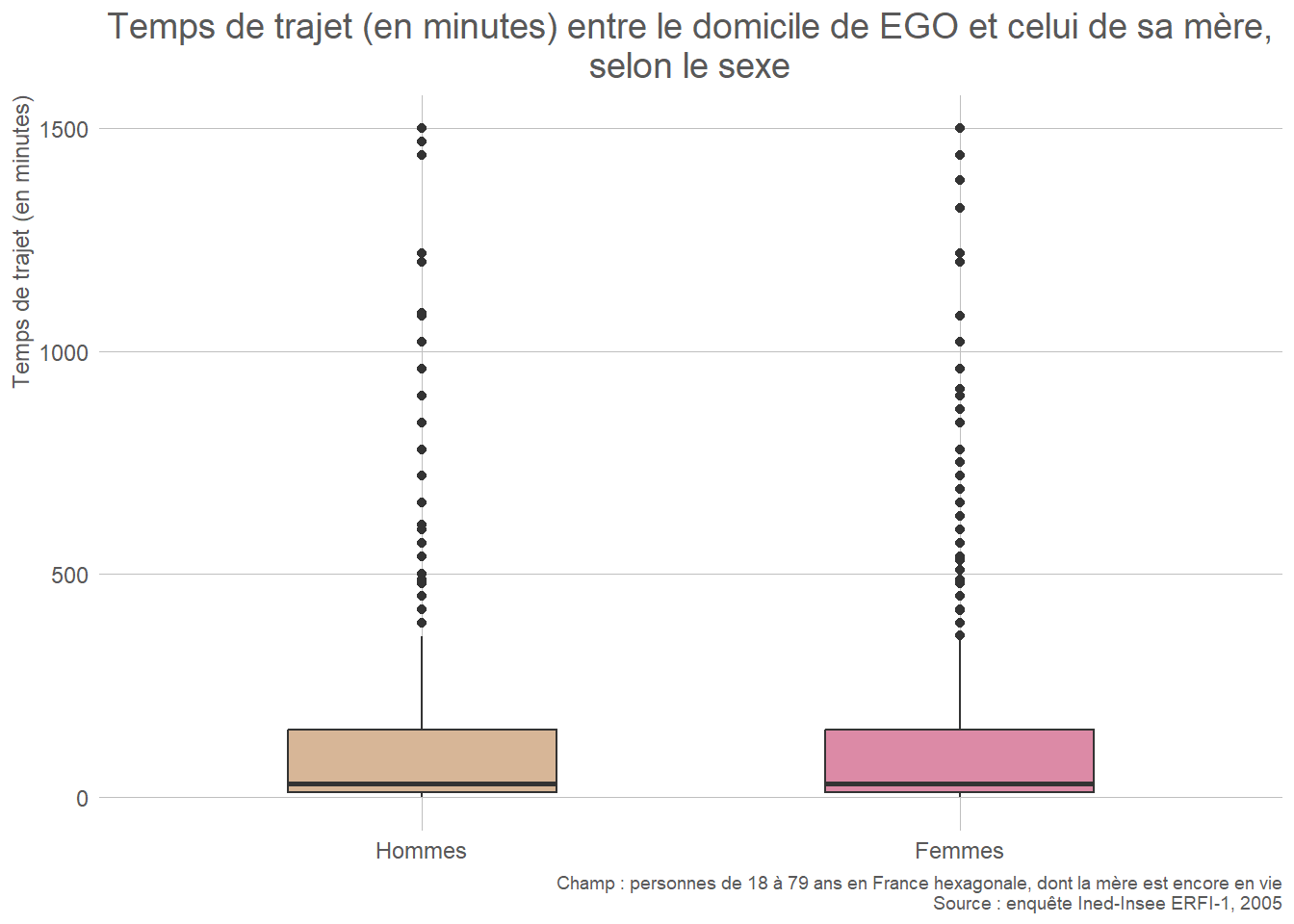
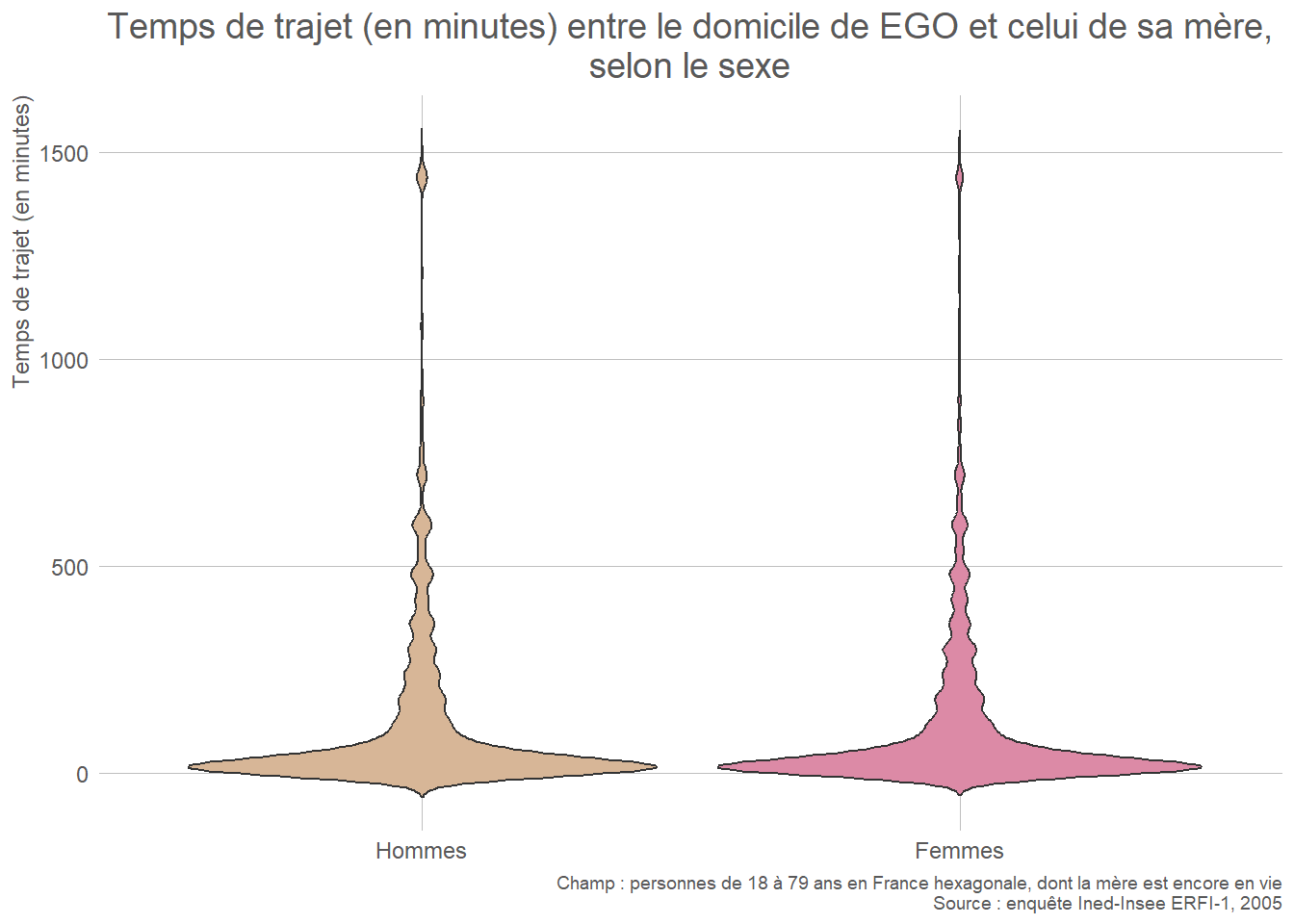
• Quantitative continue : histogramme, boîte à moustaches (box plot), diagramme en violon (violin plot).
  L’histogramme permet de visualiser la forme de la distribution. La boîte à moustaches met l’accent sur les indicateurs de position (quintiles), et permet d’identifier rapidement les points aberrants. Le diagramme en violon combine les deux représentations en ajoutant une courbe de densité autour des indicateurs de position. En revanche, les points aberrants ne sont pas aussi visibles que sur une boîte à moustache.

Représenter deux variables

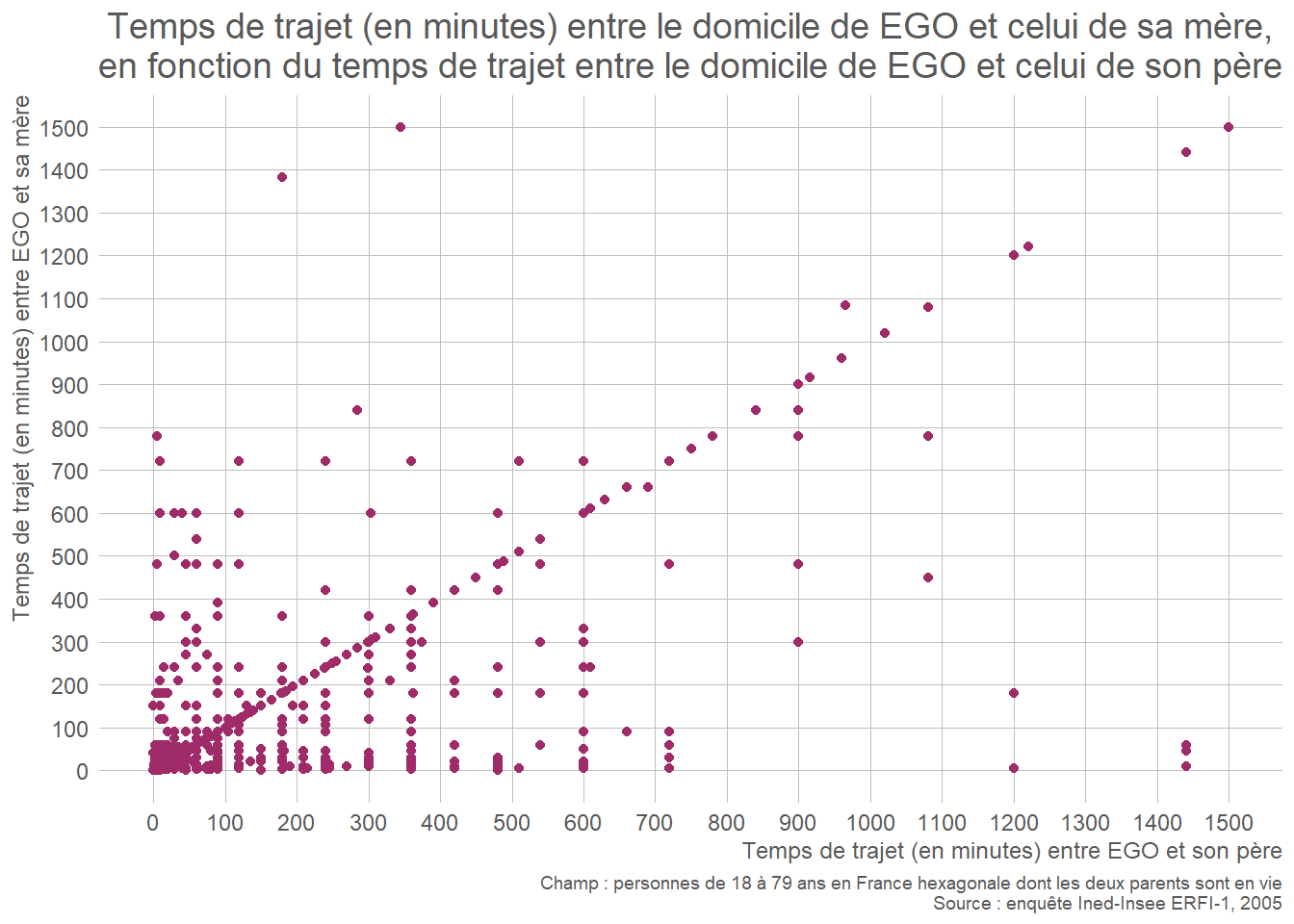
• Deux variables quantitatives : nuage de points (scatterplot)
  Cas particulier des séries temporelles : lorsque l’une des deux variables correspond à la date d’observation de la seconde variable à représenter (ex : variable 1 : année ; variable 2 : espérance de vie à la naissance). Dans ce cas, la représentation graphique appropriée est une courbe (line plot).

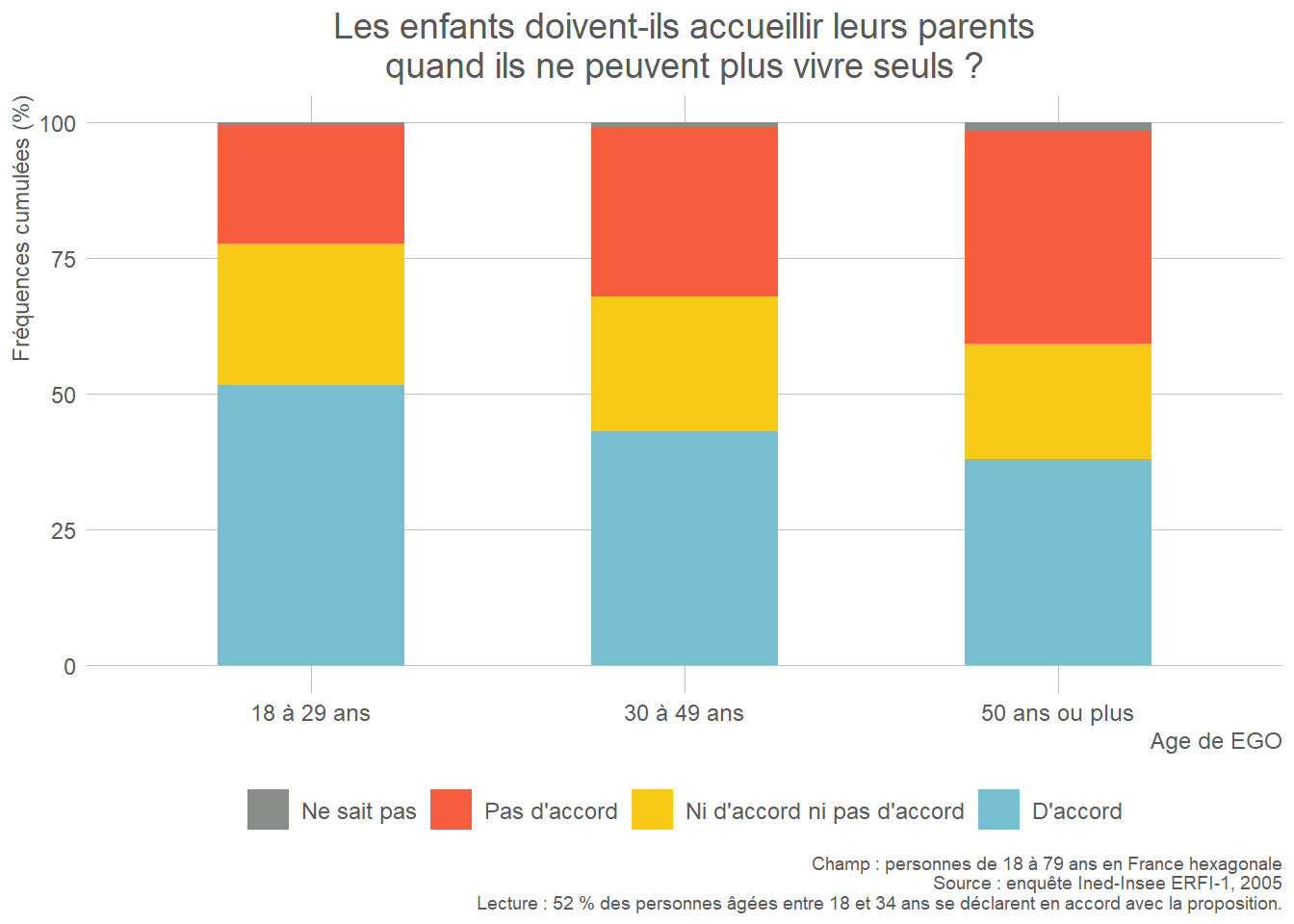
• Deux variables qualitatives OU une variable qualitative et une variable quantitative discrète : diagrammes en barres empilées (stacked barplot) ou juxtaposées (grouped barplot)
  Le choix des barres empilées ou juxtaposées dépend du nombre de modalités de la seconde variable : il est préférable de ne pas juxtaposer plus de 3 ou 4 barres.

• Une variable qualitative et une variable quantitative continue : boîtes à moustaches ou diagrammes en violon juxtaposés.

Astuce

Il existe bien d’autres types de représentations graphiques. Nous avons listé seulement les plus courants. Pour une vision plus exhaustive, le site From Data to Viz propose différentes représentations graphiques, avec les codes ggplot associés, en fonction du type de la/des variable(s) que l’on souhaite visualiser.
Gardez cependant en mémoire que les représentations graphiques les plus simples sont souvent les meilleures, car plus lisibles et plus facilement compréhensibles pour un public non spécialiste.

1.3 Principes fondamentaux de la sémiologie graphique (Jacques Bertin et ses principes : formes, couleurs, tailles, et positions pour représenter les données)

La perception d’une représentation graphique influe directement sur sa compréhension. Il est donc important de respecter un certain nombre de codes et de conventions propres à la représentation graphique de l’information, afin d’en garantir la lisibilité. Un graphique bien conçu doit permettre de transmettre un message clair et compréhensible de manière autonome, c’est-à-dire que le lecteur n’a pas besoin de se référer au texte pour comprendre ce qui est représenté.

L’ensemble des règles régissant la construction d’une représentation graphique est ce que l’on appelle la sémiologie graphique, d’après l’ouvrage de référence Sémiologie Graphique. Les diagrammes, les réseaux, les cartes, publié pour la première fois en 1967 par le cartographe français Jacques Bertin. Bien que destinées en premier lieu à la cartographie, ces règles sont applicables à toute représentation graphique d’information quantitative. Pour une version plus récente et adaptée à la représentation de données d’enquête, on peut se référer au guide de sémiologie graphique publié par l’INSEE en 2018.

Pour retranscrire l’information d’une manière adaptée à l’œil humain, Jacques Bertin a défini six variables rétiniennes, qui correspondent à différents types d’informations ou de messages à transmettre au travers de la représentation graphique :

• Taille : surface ou aire d’une forme, proportionnelle à une échelle de valeur.
  
• Valeur : positionnement dans une échelle de valeur avec dégradé de couleur, utilisé pour représenter des taux ou proportions.
  
• Couleur : utilisée pour représenter des informations de nature différente ou des valeurs ordonnées (nuancier).
  
• Forme : dessin ou pictogramme servant à qualifier la nature de l’information (surtout en cartographie, pour distinguer types de bâti, équipements, etc.).
  
• Orientation : direction de l’objet, traduisant une évolution.
  
• Grain : trame ou motif (hachures, pointillés…), pouvant se substituer aux couleurs pour une impression en noir & blanc.

Avertissement

L’usage de la 3D est fortement déconseillée, même si elle peut paraître esthétique ou plus attractive visuellement, car elle introduit une dimension qui n’existe pas dans les données. La présence d’une troisième dimension, qui n’est pas associée à un axe sur lequel on peut lire ses valeurs, complique l’interprétation et donne une représentation biaisée des données.

1.4 Rendre un graphique clair et efficace en ajoutant des éléments essentiels (titre, légende, axes, etc.).

Pour permettre la bonne compréhension du graphique indépendamment du texte qui l’accompagne, il doit être “habillé”, c’est-à-dire entouré d’un certain nombre d’éléments pour contextualiser et aider à la lecture :

• Un titre (éventuellement accompagné d’un sous-titre apportant des précisions supplémentaires) ;
  
• Un champ : quelle est la population représentée ? ;
  
• Une source : d’où sont issues les données, qui les a produites, quand ? ;
  
• Une note de lecture : une phrase reprenant l’une des valeurs du graphique, pour indiquer comment elle doit être interprétée ;
  
• Des libellés sur les axes (sans oublier les unités de mesure (ex : %, milliers)) ;
  
• Une légende : expliciter à quoi correspondent les couleurs, les tailles de points, etc.

Choisir la bonne échelle (axe des graphiques) pour représenter ses données

Il est important de choisir une échelle adaptée pour représenter ses données.
- Une échelle trop large aura tendance à “écraser” les variations ou écarts les plus faibles.
- Une échelle trop petite, au contraire, amplifie des écarts ou variations minimes.

Lorsque l’on souhaite produire plusieurs graphiques représentant le même indicateur (par exemple sur différentes sous-populations), il est essentiel d’utiliser la même échelle pour tous, afin de ne pas biaiser la comparaison.

2. Comprendre et utiliser ggplot2 pour des graphiques personnalisables et reproductibles

2.1 Introduction à ggplot2 et la “grammar of graphics”

Le package ggplot2 repose sur le concept de la grammaire des graphiques (grammar of graphics en anglais) qui représente un cadre théorique fondamental pour la visualisation des données.
Ce concept, développé par le statisticien américain Leland Wilkinson dans son ouvrage The Grammar of Graphics (1999), propose une approche structurée qui décompose chaque graphique en éléments fondamentaux distincts, organisés en couches. En construisant des graphiques étape par étape, il est ainsi possible de créer des visualisations flexibles, personnalisables et facilement modifiables.

Image inspirée de la grammaire des graphiques

Ce graphique met en évidence les principes fondamentaux de la “grammaire des graphiques”. Il montre que chaque élément d’une représentation graphique peut être conçu comme un bloc modulaire et flexible, organisé en couches superposées constituées de :

• Données (Data)
  Les données constituent le cœur de toute représentation graphique : une visualisation repose toujours sur un jeu de données, idéalement de qualité et bien structuré. Ainsi, avant même de penser à la représentation visuelle, il est essentiel de s’assurer que les données sont de qualité, correctement apurées et organisées de manière appropriée. Il est également important d’identifier les variables à représenter et leurs types, afin de choisir le mode de représentation le plus adapté.

• Esthétique (Aesthetics) ou mapping des données
  La phase d’esthétique consiste à associer les données des variables aux éléments visuels du graphique, comme les axes (x et y), les couleurs, la taille, ou encore les formes. L’esthétique définit comment les données sont traduites visuellement sur le graphique. Par exemple, dans le cas d’un graphique de dispersion (scatter plot), la variable sur l’axe X peut représenter l’âge, et celle sur l’axe Y, le nombre d’enfant(s). Des couleurs peuvent aussi être utilisées pour distinguer des sous-populations, comme par exemple les hommes et les femmes (variable sexe).

• Géométries (Geometries)
  Le terme “geometries” fait référence aux formes visuelles ou éléments graphiques (points, courbes, barres, …) utilisés pour représenter les données sur le graphique. Le choix de la géométrie dépend du type de données (quantitatives, qualitatives, continues, discrètes) et de la relation mise en évidence (ex : points pour la relation entre deux variables continues, barres pour la relation entre deux variables catégorielles, …)

• Facettes (Facets)
  Les facettes permettent de diviser un graphique en plusieurs sous-graphes basés sur les valeurs d’une autre variable. Cela permet de comparer la même représentation graphique à travers différentes catégories. C’est particulièrement utile pour analyser des sous-groupes tout en conservant la même structure graphique. Par exemple, on peut utiliser des facettes pour comparer la relation entre l’âge et le nombre d’enfants chez les hommes et les femmes, en affichant un nuage de points distinct pour chaque groupe. 

• Statistiques (Statistics)
  Des statistiques peuvent être utilisées pour construire une visualisation ou être ajoutées comme une couche supplémentaire sur un graphique (par exemple sous forme de lignes de tendance ou d’intervalles de confiance). Dans ce dernier cas, les statistiques enrichissent l’interprétation des données et ajoutent une dimension analytique au graphique.

• Coordonnées (Coordinates)
  Cette couche détermine comment les éléments visuels sont positionnés dans le graphique en fonction des valeurs des données. Le concept de coordinates fait référence au système de coordonnées utilisé pour organiser ces éléments dans l’espace du graphique. Le système de coordonnées le plus courant est le système cartésien (avec les axes x et y), mais d’autres systèmes, comme les coordonnées polaires, peuvent également être utilisés. Les coordonnées permettent aussi d’appliquer des transformations aux axes, comme l’inversion ou le changement d’échelle (par exemple, en échelle logarithmique).

• Themes (Theme)
  Cette couche concerne l’aspect esthétique global de la représentation. Elle définit des éléments comme les polices, les couleurs de fond et l’apparence des axes. Choisir un thème spécifique permet d’harmoniser l’apparence de plusieurs graphiques dans un rapport ou une présentation.

La “grammaire des graphiques” permet de construire un graphique étape par étape, en ajoutant ou modifiant chaque couche selon les besoins de l’analyse. Cette approche modulaire, sur laquelle repose ggplot2, offre une flexibilité et une puissance bien supérieures à celles d’autres outils comme Excel ou les graphiques de base R.

2.2 Avantages de ggplot2 par rapport à Excel et base R

Le package ggplot2 constitue un outil puissant pour la visualisation de données, offrant des capacités de personnalisation, de reproductibilité et de qualité graphique qui surpassent bien souvent celles d’Excel et des graphiques de base R. Ses principaux avantages sont les suivants:

• Modularité et personnalisation accrue
  Grâce à la “grammaire des graphiques” de ggplot2, chaque élément d’un graphique (titre, axes, couleurs, échelles, légendes, formes, etc.) peut être ajusté avec précision. Cela permet un contrôle détaillé, ce qui est beaucoup plus difficile avec Excel, où les options de base sont limitées et rigides. Par ailleurs, bien que la personnalisation soit possible avec base R, elle est moins intuitive et nécessite davantage de lignes de code.

• Visualisation de données complexes
  ggplot2 permet de créer des graphiques élaborés, tels que des graphiques en facettes ou des visualisations avec plusieurs variables (en jouant sur les couleurs, les formes ou les tailles). Excel peut convenir pour des jeux de données simples, mais devient rapidement limité lorsque les données sont volumineuses ou comportent plusieurs sous-groupes. base R gère bien les données complexes, mais la création de visualisations avancées demande plus d’efforts et de code, car chaque aspect du graphique doit être spécifiquement programmé.

• Automatisation et réproductibilité
  ggplot2 s’intègre facilement dans des scripts reproductibles, permettant de générer des graphiques automatiquement pour différents ensembles de données ou paramètres. Cette automatisation facilite le partage de codes et d’analyses et permet donc d’inscrire son analyse dans une démarche de science ouverte. Dans sa configuration de base, Excel, en revanche, ne permet pas d’automatiser la création de graphiques. base R permet aussi la reproductibilité des analyses et des représentations graphiques, mais avec une syntaxe moins intuitive que ggplot2, surtout pour des graphiques complexes.

• Visualisations avancées et flexibles
  Avec ggplot2, il est facile de créer des visualisations sophistiquées et esthétiques, comme des diagrammes en violon, des cartes thermiques ou des graphiques interactifs via des extensions comme plotly.
  Il est également possible d’ajouter facilement sur un graphique des lignes de tendance ou des intervalles de confiance.

Pour comparaison :
- Excel propose principalement des graphiques standards (histogrammes, nuages de points, barres), avec peu d’options pour des visualisations plus complexes.
- Base R peut produire des graphiques classiques, mais l’ajout d’éléments avancés (lignes de tendance, intervalles de confiance) est souvent plus compliqué qu’avec ggplot2.

• Communauté et évolutivité
  ggplot2 bénéficie d’une large communauté active, avec de nombreuses ressources, tutoriels et extensions. De nouvelles fonctions sont régulièrement ajoutées, ce qui permet d’étendre les capacités du package. Excel évolue plus lentement en matière de fonctionnalités graphiques, et ses outils sont limités. base R a également une communauté active, mais l’écosystème graphique est moins centralisé et cohérent qu’avec ggplot2.

Le package ggplot2 est un excellent choix pour la création de graphiques alliant flexibilité, reproductibilité et personnalisation. Le package est particulièrement adapté à l’analyse de données complexes. Il offre une grande puissance pour créer des visualisations avancées, modernes et réutilisables.

2.3 Concevoir un graphique avec ggplot2 : de la préparation à la réalisation

ggplot2 est un des packages les plus populaires du tidyverse. Comme tous les packages du tidyverse, ggplot2 respecte la philosophie des data.frames (ou tibbles) et une approche fonctionnelle unifiée, facilitant ainsi l’intégration avec d’autres outils comme dplyr ou tidyr pour permettre une analyse de données simple et cohérente.

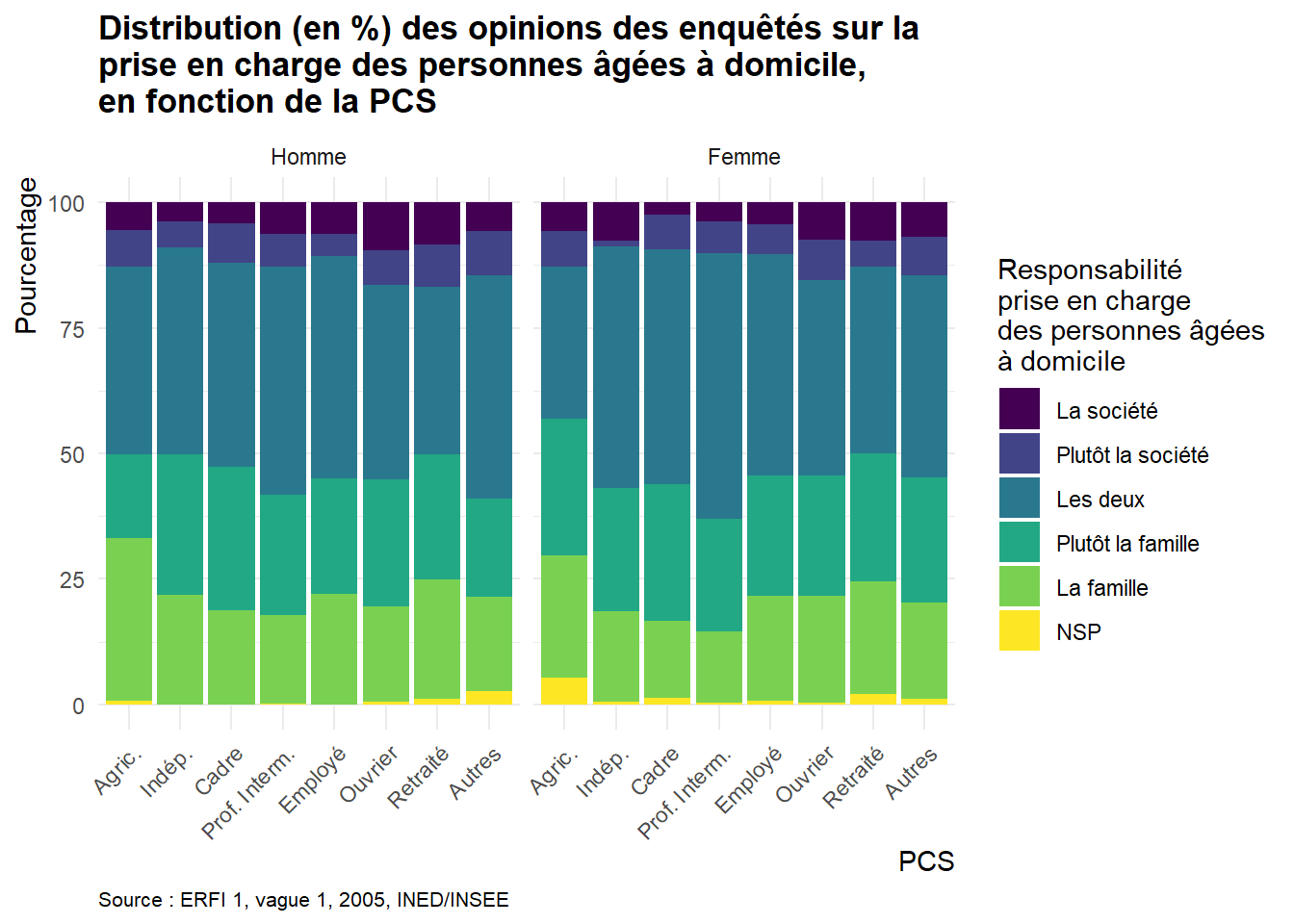
Pour découvrir, comprendre et illustrer les fonctionnalités de ggplot2, nous allons nous appuyer sur le jeu de données de la formation: ERFI1_FPA. A partir de ces données, il s’agira de créer un graphique indiquant la distribution (en %) des opinions des enquêtés sur la prise en charge des personnes âgées à domicile par la société ou la famille (variable VA_QPERSAGE dans le fichier ERFI1_FPA), en fonction de la PCS (variable AH_CS8 dans ERFI1_FPA).

2.3.1 Préparation des données

La première étape dans la création d’un graphique avec ggplot2 est de s’assurer que les données sont prêtes à être visualisées.
Pour cela, nous allons commencer par créer un nouveau projet dans RStudio (nommé ERFI_ggplot), puis charger les données de l’enquête ERFI_1 (ERFI1_FPA). Après avoir apuré les données nous calculerons les pourcentages pondérés des opinions sur la prise en charge des personnes âgées à domicile en fonction de la PCS. Les données seront ensuite remises en forme afin qu’elles soient prêtes à être représentées graphiquement avec ggplot2.

2.3.1.1 Création du projet RStudio ERFI_ggplot

Nous allons créer le projet RStudio ERFI_ggplot, qui comportera deux sous-dossiers pour organiser efficacement nos fichiers :

• data : Dans ce dossier, nous placerons le fichier .csv contenant les données de l’enquête (ERFI1_FPA.csv). Ce fichier est disponible dans l’onglet Matériel, puis dans le menu Bases de données du site de la formation.
• script : Dans ce dossier, nous enregistrerons les scripts où nous réaliserons les applications et les exercices liés à la formation.

Pour créer le projet RStudio ERFI_ggplot, deux méthodes peuvent être utilisées :

1. Via le menu
   Il est possible de passer par le menu de RStudio en sélectionnant File, puis New Project. À ce stade, il vous sera demandé si vous souhaitez créer un nouveau répertoire pour le projet ou utiliser un répertoire existant. Si vous choisissez de créer un nouveau répertoire, vous devrez spécifier l’emplacement et le nom du projet. Ensuite, vous pourrez créer les sous-dossiers mentionnés.

2. Directement par un script
   Une autre option consiste à créer le projet et ses sous-dossiers en utilisant un script R. Cette méthode peut être plus rapide et efficace, surtout lorsque on est à l’aise avec la programmation. Voici le script qui permet de créer directement le projet ERFI_ggplot ainsi que les sous-dossiers mentionnés. Une fois le projet créé, il sera nécessaire d’ajouter manuellement les fichiers correspondants dans chacun des sous-dossiers.

# Définir le nom et le chemin du projet 
# (avec l'option getwd(), le projet sera par défaut créé dans le répertoire courant)
project_name <- "ERFI_ggplot"
project_path <- file.path(getwd(), project_name)

# Création du dossier du projet
dir.create(project_path, recursive = TRUE)

# Créer les sous-dossiers 'data', 'doc', 'support', 'script'
dir.create(file.path(project_path, "data"), recursive = TRUE)
dir.create(file.path(project_path, "script"), recursive = TRUE)

# Création d'un fichier de projet RStudio (.Rproj) en y ajoutant directement les sous-dossiers
file_path_rproj <- file.path(project_path, paste0(project_name, ".Rproj"))
writeLines(c("Version: 1.0"), con = file_path_rproj)

# Installation de rstudioapi si ce n'est pas déjà fait
if (!requireNamespace("rstudioapi", quietly = TRUE)) {
  install.packages("rstudioapi")
}

# Ouvrir le projet ERFI_ggplot dans RStudio
if (requireNamespace("rstudioapi", quietly = TRUE)) {
  rstudioapi::openProject(project_path)
} else {
  message("Le package 'rstudioapi' est requis pour ouvrir le projet automatiquement.")
}

# Ajouter manuellement le fichier "ERFI1_FPA.csv" dans le sous-dossier data du projet ERFI_ggplot que vous venez de créer dans le répertoire courant (dossier dans lequel R cherche et sauvegarde les fichiers par défaut. Pour afficher le répertoire courant, vous pouvez utiliser la fonction getwd() 

Vous pouvez ensuite ouvrir un nouveau script dans le projet ERFI_ggplot en cliquant sur File (Fichier) dans la barre de menu. Sélectionnez New File (Nouveau fichier) puis R Script. Vous pouvez aussi utiliser le raccourci clavier Ctrl + Shift + N (ou Cmd + Shift + N sur Mac) pour ouvrir directement un nouveau script.

2.3.1.2 Chargement des données ERFI_1

La fonction library() permet de charger les packages.

library(readr)
ERFI1_FPA <- read_csv("data/ERFI1_FPA.csv")

2.3.1.3 Installation et chargement des packages

Pour pouvoir utiliser ggplot2 ainsi que tous les packages nécessaires aux étapes préalables à la représentation graphique, comme l’apurement et la mise en forme des données, il est recommandé de télécharger le package tidyverse. Ce dernier regroupe plusieurs packages essentiels tels que ggplot2 mais aussi dplyr pour l’apurement et la manipulation des données, tidyr pour la mise en forme des données (transformation en format long ou large), et beaucoup d’autres outils complémentaires. Il est également possible de télécharger le package questionr qui facilite la manipulation, le recodage et l’analyse de données d’enquêtes.

#Installation des packages tidyverse et questionr s'ils ne sont pas déjà installés

if (!require(tidyverse)) install.packages("tidyverse", dependencies = TRUE, repo="http://cran.rstudio.com/")
if (!require(questionr)) install.packages("questionr", dependencies = TRUE, repo="http://cran.rstudio.com/")

Il s’agit désormais de charger les packages tidyverse et questionrgrâce à l’instruction library.

library(tidyverse)
library(questionr)

2.3.1.4 Gestion des données manquantes et des modalités peu représentées

On parle de donnée manquante dans une enquête lorsque la valeur associée à la réponse d’un enquêté pour une variable spécifique n’est pas disponible. La gestion des données manquantes est une étape cruciale dans tout projet d’analyse de données. Les données manquantes peuvent influencer les résultats des analyses et mener à des interprétations erronées.
ggplot2 ne gère pas automatiquement les données manquantes ², il est donc essentiel de traiter les données manquantes (suppression, imputation, …) avant de mener des analyses ou de créer des visualisations à partir d’un jeu de données.

#Sélection des variables utiles pour l'analyse (en conservant la variable sexe pour un exemple ultérieur)
exemple1 <- select(ERFI1_FPA, VA_QPERSAGE, AH_CS8, MA_SEXE, poids12)

#Exploration du nombre de données manquantes pour chaque variable avec la fonction table et l'option (useNA= = "always")

#Opinion sur la responsabilité de la prise en charge des personnes âgées
table(exemple1$VA_QPERSAGE, useNA = "always")

   1    2    3    4    5    9 <NA> 
 640  673 4200 2469 2005   92    0 

#PCS
table(exemple1$AH_CS8, useNA = "always")

   1    2    3    4    5    6    7    8    9 <NA> 
 128  326  735 1715 1956 1393 2548 1277    1    0 

#Sexe
table(exemple1$MA_SEXE, useNA = "always")

   1    2 <NA> 
4371 5708    0 

Pour les variables d’intérêt, il n’y a pas de données manquantes dans le jeu de données exemple1.

L’analyse des tableaux de distribution montre que chacune des modalités est assez bien représentée dans les données pour la variable VA_QPERSAGE. En revanche, la modalité “9” (“Non codé”) de la variable AH_CS8 ne concerne qu’un seul individu. Il est donc raisonnable d’éliminer cette modalité ainsi que l’individu concerné de l’analyse.

#Eliminer les individus dont la modalité de la variable exemple1$AH_CS8 = "9" avec la fonction filter

exemple1 <- filter(exemple1, (AH_CS8 != 9))

#Vérifier que la modalité a disparu des données en regardant le nombre de lignes du jeu de données

dim(exemple1)

[1] 10078     4

Traitement des données manquantes

Dans cet exemple, il n’y pas de données manquantes.
Lorsque les données manquantes sont peu nombreuses, on peut se contenter d’exclure les individus concernés en utilisant par exemple les fonctions filter() et complete.cases() pour conserver uniquement les lignes sans données manquantes (filter(mydata, complete.cases(mydata)). On peut également choisir de regrouper les modalités peu fréquentes avec d’autres, en suivant une logique pertinente.
Cependant, lorsque les valeurs manquantes concernent un plus grand nombre d’individus, il est essentiel de les analyser pour comprendre leur origine et vérifier si les non-répondants partagent un profil particulier. En fonction des résultats de cette analyse, il peut être judicieux de conserver les données manquantes dans l’analyse en créant une catégorie spécifique pour les non-réponses, ou d’utiliser des procédures d’imputation.
L’imputation consiste à remplacer une valeur manquante par une valeur “probable”, extrapolée à partir des réponses d’individus présentant des caractéristiques similaires à celles de l’individu pour qui la donnée est manquante.
Quelques pistes d’analyse des données manquantes sont explorées dans cet article. S’agissant des méthodes pour traiter les données manquantes il est possible de se référer à ce tutoriel ou bien à celui-ci.

2.3.1.5 Choix des éléments à représenter et calcul de statistiques descriptives

Dans cet exemple, nous souhaitons représenter graphiquement la proportion de personnes exprimant des avis différents sur la question de qui devrait prendre en charge les personnes âgées à domicile, avec des réponses allant de principalement la société à principalement la famille (1 = “La société”, 2 = “Plutôt la société”, 3 = “Les deux”, 4 = “Plutôt la famille”, 5 = “La famille”) en incluant la modalité 9 = “Ne sait pas” (variable VA_QPERSAGE), selon la PCS (variable AH_CS8).
Il s’agit donc de construire un tableau croisé indiquant en ligne la PCS des enquêtés (variable AH_CS8) et en colonne les différentes opinions concernant qui doit prendre en charge les personnes âgées en domicile (variable VA_QPERSAGE). Comme nous souhaitons comparer les PCS entre-elles et que celles-ci vont figurer en lignes dans le tableau construit, nous calculerons des pourcentages lignes.
A l’intersection des lignes et des colonnes, le tableau doit fournir la distribution (en pourcentage) des personnes en fonction des deux variables considérées. Comme nous utilisons les données d’une enquête réalisée auprès d’un échantillon représentatif de la population, il ne faut pas oublier d’utiliser la variable de pondération (poids12) pour calculer ces pourcentages. 

La fonction wtd.table du package questionr permet de réaliser des tableaux croisés en tenant compte de la pondération, avec l’argument weights.

# Avec le package questionr, en utilisant la fonction `wtd.table()` qui prend trois arguments : 
# 1- La variable à représenter sur les lignes du tableau croisé (ici AH_CS8),
# 2- La variable à représenter sur les colonnes du tableau croisé (ici VA_QPERSAGE),
# 3- La variable de pondération avec l'argument weights (ici poids12)

#Puis calcul des pourcentages en ligne avec lprop() puisque nous souhaitons comparer les opinions entre les tranches d'âges.
Opinion_PCS <- wtd.table(exemple1$AH_CS8, exemple1$VA_QPERSAGE, weights = exemple1$poids12) |> 
  lprop()

Calcul des pourcentages pondérés avec dplyr

Il est également possible de calculer les proportions pondérées des opinions sur la prise en charge des personnes âgées en fonction de la PCS avec le package dplyr

Opinion_PCS <- exemple1  |> 
  group_by(AH_CS8, VA_QPERSAGE) |>   # Regrouper les données par PCS (AH_CS8) et par opinion (VA_QPERSAGE)
  summarise(
    n = sum(poids12),  # Calcul de la somme des poids (POND) pour chaque combinaison de PCS et d'opinion
    .groups = "drop"  # Ne pas conserver les groupes après le résumé 
  ) |> 
  group_by(AH_CS8) |>  # Regrouper à nouveau par PCS (AH_CS8) pour calculer les proportions
  mutate(proportion = n / sum(n))  # Calculer la proportion pondérée en divisant n par la somme de n pour chaque PCS

# Afficher les résultats finaux contenant les proportions pondérées
print(Opinion_PCS)  

2.3.1.6 Format des données

Pour pouvoir être visualisées à l’aide de ggplot2, les données doivent être sous forme de data.frame (ou tibble). Dans un data.frame, chaque ligne du tableau correspond à une observation, et chaque colonne représente une variable.

Organisation des données dans un data.frame

Il est possible de vérifier qu’un objet R est un data frame en utilisant les fonctions is.data.frame() (qui doit retourner TRUE), class() ou str().

is.data.frame(Opinion_PCS)

[1] FALSE

class(Opinion_PCS)

[1] "proptab" "table"  

L’objet Opinion_PCS n’est pas un data.frame mais un objet table. Pour changer la classe d’un objet en data.frame on peut utiliser la fonction as.data.frame()

Opinion_PCS <- as.data.frame(Opinion_PCS)

class(Opinion_PCS)

[1] "data.frame"

head(Opinion_PCS)

  Var1 Var2     Freq
1    1    1 5.594084
2    2    1 5.004533
3    3    1 3.540504
4    4    1 5.032790
5    5    1 4.761471
6    6    1 9.140570

L’objet Opinion_PCS est désormais de classe data.frame. Les noms des variables de ce data.frame à savoir Var1 et Var2 ne sont cependant pas du tout explicites, il est préférable de les renommer. La fonction rename() permet de remplacer le nom Var1 par celui de PCS, et le nom Var2 par celui de Opinion.

Opinion_PCS <- as.data.frame(Opinion_PCS) |> 
  rename(
    PCS = Var1,          # Remplacer Var1 par le nom "PCS"
    Opinion = Var2       # Remplacer Var2 par le nom "Opinion"
  )

head(Opinion_PCS)

  PCS Opinion     Freq
1   1       1 5.594084
2   2       1 5.004533
3   3       1 3.540504
4   4       1 5.032790
5   5       1 4.761471
6   6       1 9.140570

Maintenant que notre objet Opinion_PCS est un data.frame on peut aussi supprimer les marges du tableau croisé ajoutées automatiquement lors de la création d’un tableau croisé avec la fonction wtd.table car elles ne sont pas pertinentes pour la représentation graphique. Il s’agit de la modalité “Total” de la variable Opinion et de la modalité “Ensemble” de la variable PCS. On utilise pour cela la fonction filter du package dplyr inclut dans le tidyverse.

Opinion_PCS <- Opinion_PCS |> 
  filter(!(Opinion == "Total" | PCS == "Ensemble"))

2.3.1.7 Format long : organisation des variables dans un data.frame pour ggplot2

Le format long et le format large sont deux façons de structurer des données dans un data.frame. Ces formats sont essentiels à comprendre car ils influencent la manière dont on peut analyser et visualiser les données, notamment avec des outils comme ggplot2.

• Format large (wide format)
  Dans le format large, les données sont organisées de façon que chaque colonne représente une variable différente, et chaque ligne représente une observation unique. Ce format est souvent utilisé pour des résumés ou des tableaux de résultats, mais il est moins flexible pour les analyses plus complexes ou les visualisations graphiques.

Exemple
Imaginons que nous avons des données sur le nombre de visites au domicile de la mère pour deux années: 2000 et 2005. En format large, nous aurions une colonne pour chaque année comme ceci :

ID	visites_2000	visites_2005
1	5	10
2	8	9
3	3	3

Ici, chaque individu (ID) est sur une ligne et chaque colonne représente une variable : le nombre de visites au domicile de la mère une année donnée, visites_2000 pour l’année 2000 et visites_2005 pour l’année 2005.

• Format long (long format)
  Dans le format long, les données sont réorganisées de manière à ce que chaque ligne corresponde à une seule observation d’une variable donnée, et toutes les modalités de cette variable sont regroupées dans une seule colonne. Le format long est souvent préféré pour les analyses statistiques et les visualisations, car il est plus facile à utiliser pour représenter des relations entre variables.

Dans l’exemple présenté plus haut, au lieu d’avoir une colonne différente pour chaque mesure du nombre de visites au domicile de la mère (2000 puis 2005), on réorganise les observations sur le nombre de visites au domicile sur plusieurs lignes, et on ajoute une colonne pour indiquer les différents niveaux de la variable (ici l’année 2000 ou 2005).

Dans un format long , le jeu de données exemple ressemble ainsi à ceci :

ID	Année	Visites
1	2000	5
1	2005	10
2	2000	8
2	2005	9
3	2000	3
3	2005	3

ggplot2 est basé sur la grammaire des graphiques, qui nécessite que les données soient organisées en format long. Il faudra donc transformer un data.frame en format large en data.frame en format long pour pouvoir réaliser une visualisation graphique à partir de ggplot2.

Dans le data.frame Opinion_PCS contenant les proportions pondérées des opinions sur la prise en charge des personnes âgées en fonction de la PCS, les données sont structurés de la manière suivante :

head(Opinion_PCS, 10)

   PCS Opinion     Freq
1    1       1 5.594084
2    2       1 5.004533
3    3       1 3.540504
4    4       1 5.032790
5    5       1 4.761471
6    6       1 9.140570
7    7       1 8.025316
8    8       1 6.462146
9    1       2 7.169817
10   2       2 3.935733

Dans ce data.frame, chaque ligne représente une situation unique, associant une catégorie socioprofessionnelle (PCS) à une opinion (Opinion). Les valeurs (ici, les proportions dans la colonne Freq) sont placées dans une seule colonne, plutôt que d’être réparties dans plusieurs colonnes correspondant à chaque opinion.
Cette structure correspond au format long. Le data.frame Opinion_PCS est donc déjà organisé dans ce format, et il n’est pas nécessaire de le convertir. Cependant, cela n’est pas toujours le cas pour d’autres jeux de données.

Lorsque les données à représenter sont organisées en format large, il faut utiliser la fonction pivot_longer() pour les convertir.
Sa syntaxe est la suivante:

pivot_longer(data, cols, names_to, values_to)

Ses principaux arguments sont:

• data : le nom de l’objet à transformer,
• cols : le nom des colonnes à transformer. On peut spécifier les colonnes avec leurs noms en utilisant le vecteur c() et en séparant ces noms par une virgule s’il y en a plusieurs ou utiliser des fonctions d’aide à la sélection (telles que starts_with(), ends_with(), etc.). Il est aussi possible d’exclure certaines colonnes de la conversion grâce à l’opérateur -,
• names_to : le libellé de la nouvelle colonne qui contiendra les noms des colonnes d’origine (avant la transformation),
• values_to : le nom de la nouvelle colonne qui contiendra les valeurs des colonnes d’origine.
  

Exemple

Si les données du data.frame Opinion_PCS étaient organisées en format large, chaque colonne représenterait une opinion différente (les niveaux de la variable Opinion), et chaque ligne correspondrait à une catégorie socioprofessionnelle (PCS). Autrement dit, pour chaque PCS, on retrouverait plusieurs colonnes contenant les pourcentages associés à chaque opinion.
Le tableau de données ressemblerait donc à ceci :

# A tibble: 6 × 7
  PCS     `1`   `2`   `3`   `4`   `5`   `9`
  <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1      5.59  7.17  34.9  20.5  29.4 2.44 
2 2      5.00  3.94  43.5  26.8  20.7 0.146
3 3      3.54  7.42  43.1  28.0  17.5 0.531
4 4      5.03  6.48  49.2  23.1  15.9 0.288
5 5      4.76  5.62  44.1  23.8  21.2 0.580
6 6      9.14  7.04  38.8  25.2  19.4 0.434

La syntaxe suivante permet de transformer ces données du format large au format long à l’aide de la fonction pivot_longer() :

Opinion_PCS_longer <- Opinion_PCS_large |> #Le nom du *data.frame* en format large
  pivot_longer(
    cols = -PCS,  # Exclure la colonne PCS de la conversion
    names_to = "Opinion",  # Nommer la nouvelle colonne contenant les différents niveaux/modalités d'opinion
    values_to = "Proportion"  # Nommer la nouvelle colonne contenant les proportions
  )

head(Opinion_PCS_longer)

# A tibble: 6 × 3
  PCS   Opinion Proportion
  <fct> <chr>        <dbl>
1 1     1             5.59
2 1     2             7.17
3 1     3            34.9 
4 1     4            20.5 
5 1     5            29.4 
6 1     9             2.44

2.3.1.8 Types de vecteurs

Les variables catégorielles (comme PCS ou Opinion) correspondent à des données qui prennent des valeurs distinctes et limitées, souvent désignées par des codes (tels que 1, 2, 3, 4, etc.), au format numérique, ou par des noms (comme “Agriculteur”, “Artisans, commerçants et chefs d’entreprise”, “Employés”, “Ouvriers”, “Retraités”, etc.), au format caractère. Dans ggplot2, ces variables peuvent être utilisées directement pour créer la plupart des graphiques, sans transformation préalable.
Cependant, si vous souhaitez contrôler l’ordre d’affichage des catégories dans vos graphiques, il est utile de transformer ces variables en un type de donnée spécial appelé facteur. Cette transformation permet de définir un ordre personnalisé aux catégories ou modalités d’une variable, car par défaut, ces dernières sont affichées par ordre alphabétique ou numérique. En transformant une variable en facteur, vous pouvez par exemple choisir d’afficher “Employés” (code 5) et “Ouvriers” (code 6) en premier sur le graphique, au lieu d’ “Agriculteur” (code 1) et “Artisans, commerçants et chefs d’entreprise” (code 2).

Dans notre exemple, vérifions comment les variables catégorielles, PCS et Opinion, sont traitées à l’aide de la fonction str().

str(Opinion_PCS)

'data.frame':   48 obs. of  3 variables:
 $ PCS    : Factor w/ 9 levels "1","2","3","4",..: 1 2 3 4 5 6 7 8 1 2 ...
 $ Opinion: Factor w/ 7 levels "1","2","3","4",..: 1 1 1 1 1 1 1 1 2 2 ...
 $ Freq   : num  5.59 5 3.54 5.03 4.76 ...

Dans l’objet Opinion_PCS, les variables PCS et Opinion sont déjà traitées comme des facteurs. Si cela n’était pas déjà le cas, la fonction factor() permet de transformer une variable catégorielle en facteur.

# Transformer les variables PCS et Opinion en facteurs 

Opinion_PCS$PCS <- factor(Opinion_PCS$PCS)
Opinion_PCS$Opinion <- factor(Opinion_PCS$Opinion)

La fonction factor() permet de gérer l’ordre d’apparition des catégories dans un graphique et d’associer des labels aux catégories, plutôt que de les créer directement dans ggplot2.

#Pour la variable Opinion
Opinion_PCS$Opinion <- factor(Opinion_PCS$Opinion, 
                                levels = c(1, 2, 3, 4, 5, 9), 
                                labels = c("La société", 
                                           "Plutôt la société", 
                                           "Les deux", 
                                           "Plutôt la famille", 
                                           "La famille", 
                                           "NSP"))
# Pour la variable PCS
Opinion_PCS$PCS <- factor(Opinion_PCS$PCS, 
                             levels = c(1, 2, 3, 4, 5, 6, 7, 8),  
                             labels = c("Agric.", 
                                        "Indep" ,
                                        "Cadre" , 
                                        "Prof. Interm." ,
                                        "Employé",
                                        "Ouvrier",
                                        "Retraité",
                                        "Autres"))

Les données sont désormais prêtes pour être visualisées à partir de ggplot2.

2.3.2 Mécanique et syntaxe de ggplot2 : création d’un graphique étape par étape

Cette section présente les principes fondamentaux de ggplot2 et la manière de construire un graphique en suivant la “grammaire des graphiques”.
Nous allons d’abord explorer la logique sous-jacente de cette grammaire et détailler chaque étape du processus, de l’association des variables aux axes à l’exportation du graphique final. L’objectif est de montrer comment chaque “calque” du graphique se superpose pour créer une visualisation claire et précise.

2.3.2.1 Principe de base : la grammaire des graphiques avec ggplot2

Le concept fondamental sur lequel repose ggplot2 est la grammaire des graphiques. Cette approche consiste à assembler des calques successifs (layers) pour construire un graphique. Chacun des calques peut ajouter des éléments à la représentation graphique, comme des points, des lignes, ou des statistiques, etc. , et plusieurs calques sont empilés pour produire une visualisation complète. 

Dans la fonction ggplot2, les calques sont empilés à l’aide de l’opérateur + placé à la fin de chaque ligne pour améliorer la lisibilité.

Création d’un graphique ggplot2 par ajout de couches successives

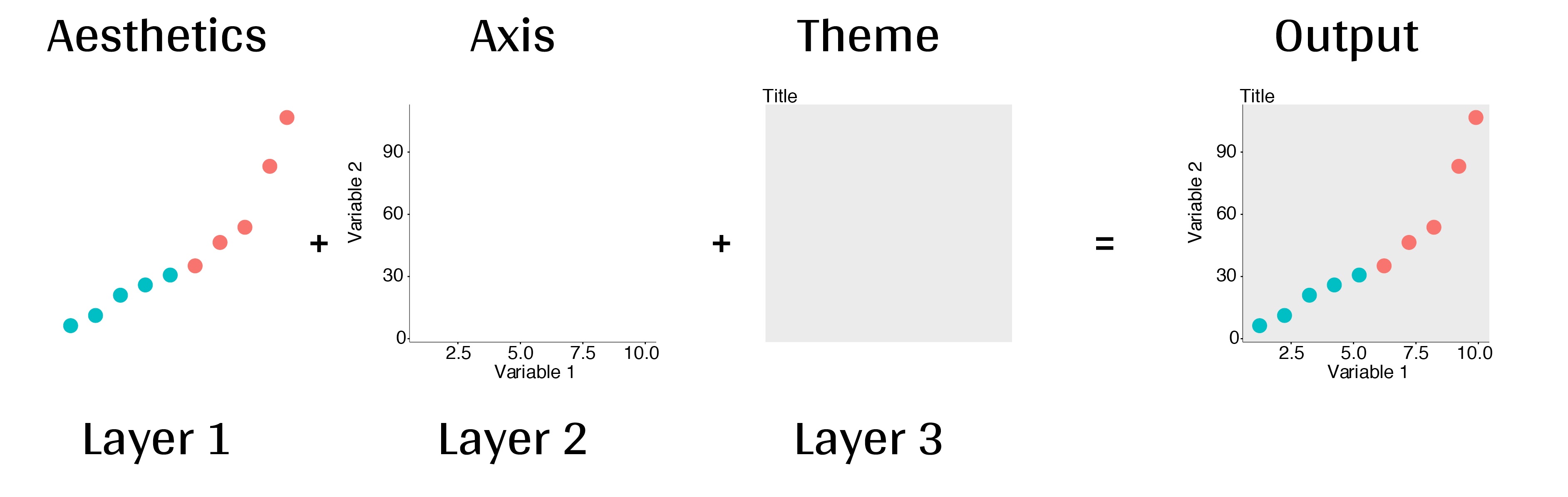
2.3.2.2 Les étapes de création d’un graphique avec ggplot2 

Cette sous-partie présente les étapes nécessaires à la création d’un graphique avec ggplot2, en appliquant la logique de la grammaire des graphiques. Chaque étape correspond à un calque, qui, assemblé progressivement, permet de construire la visualisation finale. 

Pour illustrer ce processus, la démonstration s’appuie sur un exemple concret basé sur des données issues de l’enquête ERFI-1. Le graphique final représentera les proportions pondérées (Freq) des opinions sur la prise en charge des personnes âgées (Opinion) selon la catégorie socioprofessionnelle (PCS) des enquêtés (PCS). Les données nécessaires ont été préalablement calculées et regroupées dans le data.frame Opinion_PCS.

En complément, un deuxième exemple, plus simple, illustrant les pourcentages pondérés (Freq) d’enquêtés en fonction de l’âge (MA_AGEM_rec, variable continue) et du sexe (MA_SEXE, variable catégorielle) permet d’explorer certaines fonctions spécifiques aux graphiques linéaires.

2.3.2.2.1 Sélectionner le jeu de données à utiliser pour la représentation  

La première étape de la construction d’un graphique avec ggplot2 consiste à indiquer le jeu de données qui contient les données à visualiser. Ce jeu de données doit être organisé sous forme de data.frame et structuré au format long, où chaque ligne représente une observation unique et chaque colonne correspond à une variable. 

L’exemple utilisé ici s’appuie sur le data.frame Opinion_PCS, qui contient :

• La variable Opinion, contenant les opinions des enquêtés sur qui, de la famille ou de la société, doit prendre en charge des personnes âgées à domicile.
• La variable PCS, indiquant la catégorie socioprofessionnelle des enquêtés.
• La variable Freq, représentant les proportions pondérées relatives aux modalités de la variable Opinion.
  

Pour préciser que c’est le jeu de données Opinion_PCS qui contient les variables à représenter, il faut utiliser l’argument data dans la fonction ggplot() :

ggplot(data=Opinion_PCS)

#On peut également préciser uniquement le data.frame sans utiliser l'argument data=

ggplot(Opinion_PCS)

2.3.2.2.2 Associer les variables aux axes x et y  

Il est ensuite nécessaire de spécifier quelles variables du jeu de données seront représentées sur les axes X et Y du graphique. Cette étape permet de définir la structure de base de la visualisation.

La fonction aes() (aesthetics) est utilisée pour associer les variables aux axes. Dans aes(), vous devez indiquer les noms des colonnes du data.frame correspondant à :

• L’axe des abscisses (x)
• L’axe des ordonnées (y).

Dans l’exemple, à partir du data.frame Opinion_PCS, il s’agit de créer un graphique où :

• La variable PCS (PCS) est représentée sur l’axe X.
• La variable des proportions pondérées des opinions (Freq) est représentée sur l’axe Y.
  

Pour associer ces variables aux axes x et y, l’instruction ggplot2 est la suivante:

ggplot(Opinion_PCS, aes(x = PCS, y = Freq))

À ce stade, aucun graphique n’est encore dessiné. Ce code initialise simplement une trame où : l’axe X est étiqueté avec les valeurs de la colonne (PCS) et l’axe Y est étiqueté avec les valeurs de la colonne (Freq).

2.3.2.2.3 Personnaliser les éléments visuels du graphique : couleur, remplissage et type de ligne  

Une fois que les variables ont été associées aux axes X et Y, il est possible de personnaliser l’apparence du graphique pour le rendre plus lisible et compréhensible. Ces personnalisations permettent de modifier des éléments tels que la couleur, la forme, le remplissage ou le type de ligne.

Ces options sont particulièrement utiles pour différencier les catégories ou améliorer l’esthétique du graphique. Par exemple, il est possible d’attribuer une couleur distincte à chaque catégorie ou d’utiliser des formes différentes pour représenter divers groupes.

Dans ggplot2, l’apparence des éléments graphiques est contrôlée à travers l’argument aes() (aesthetics). Voici quelques arguments visuels courants dans aes() :

• color : Définit la couleur des éléments graphiques, comme les contours des barres ou des points. Vous pouvez spécifier une couleur fixe (par exemple, “red”) ou lier la couleur à une variable pour différencier des catégories visuellement.

Exemple
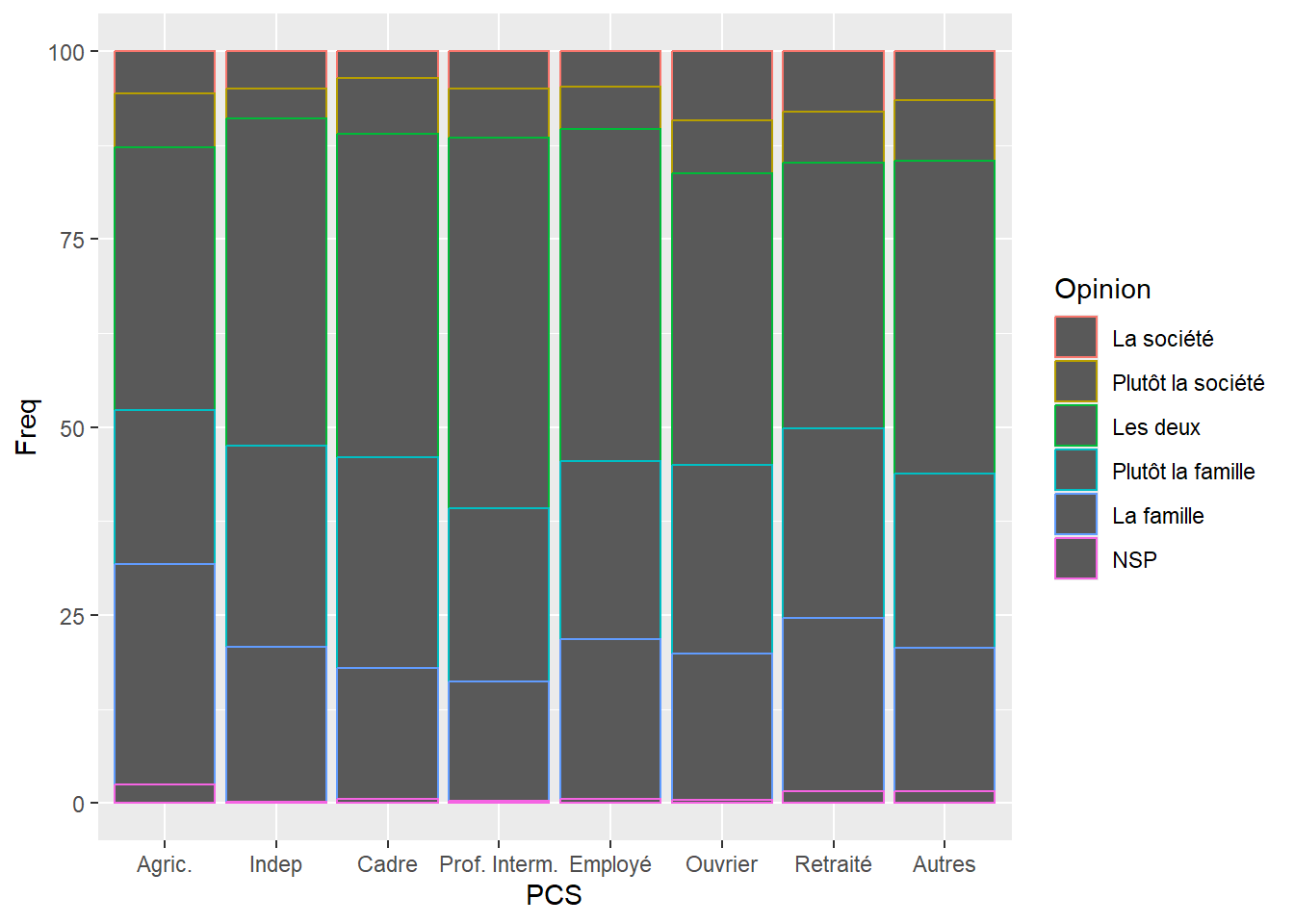
Répartition des opinions relatives à la prise en charge des personnes âgées en fonction de la PCS en faisant varier la couleur de contour des barres en fonction des modalités de la variable Opinion

• fill : Cet argument détermine la couleur intérieure des formes fermées, comme les barres d’un diagramme à barres, les points dans un nuage de points ou des formes dans des diagrammes à secteurs. Contrairement à color, qui pourrait affecter la bordure d’une géométrie, fill modifie juste la couleur de l’intérieur des formes.
  

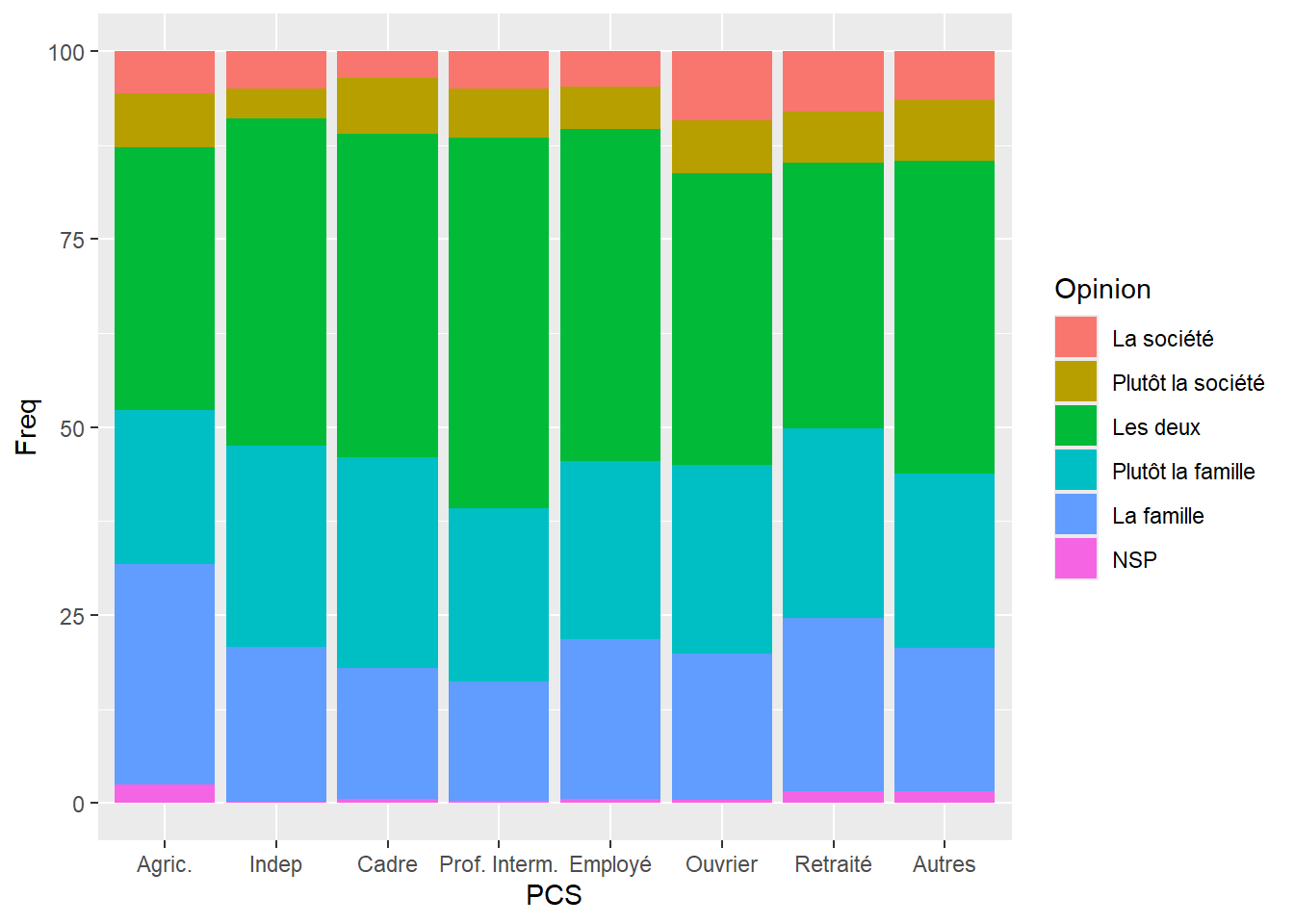
Exemple

Répartition des opinions relatives à la prise en charge des personnes âgées en fonction de la PCS en faisant varier la couleur de fond des barres en fonction des modalités de la variable Opinion

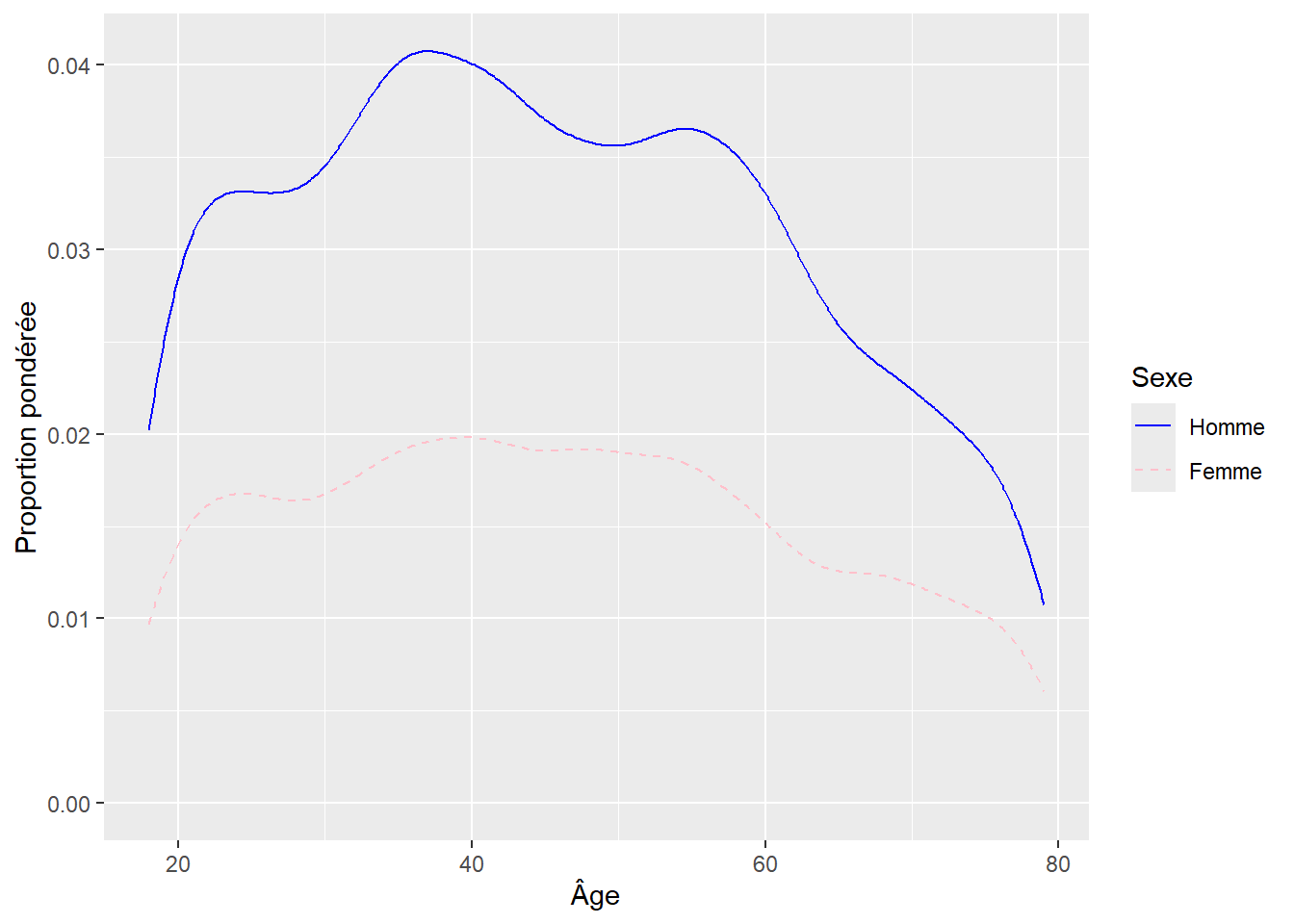
• linetype : Détermine le style de ligne pour les éléments comme les courbes ou les lignes de tendance. Par défaut, les types de ligne sont “solid” (trait plein), “dashed” (tiret) ou “dotted” (pointillé). Il est aussi possible de lier linetype à une variable pour différencier plusieurs courbes dans un même graphique.
  

Exemple
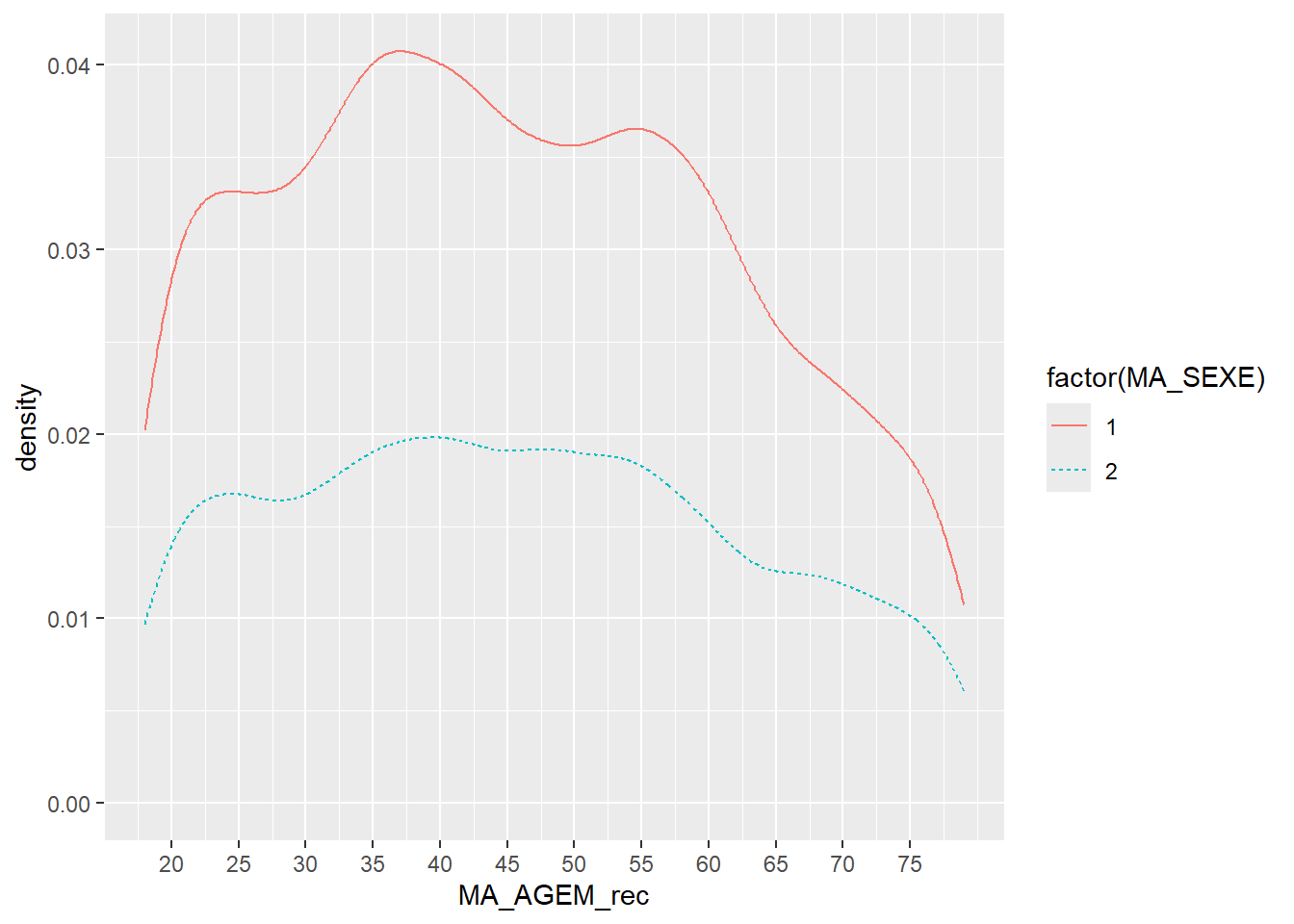
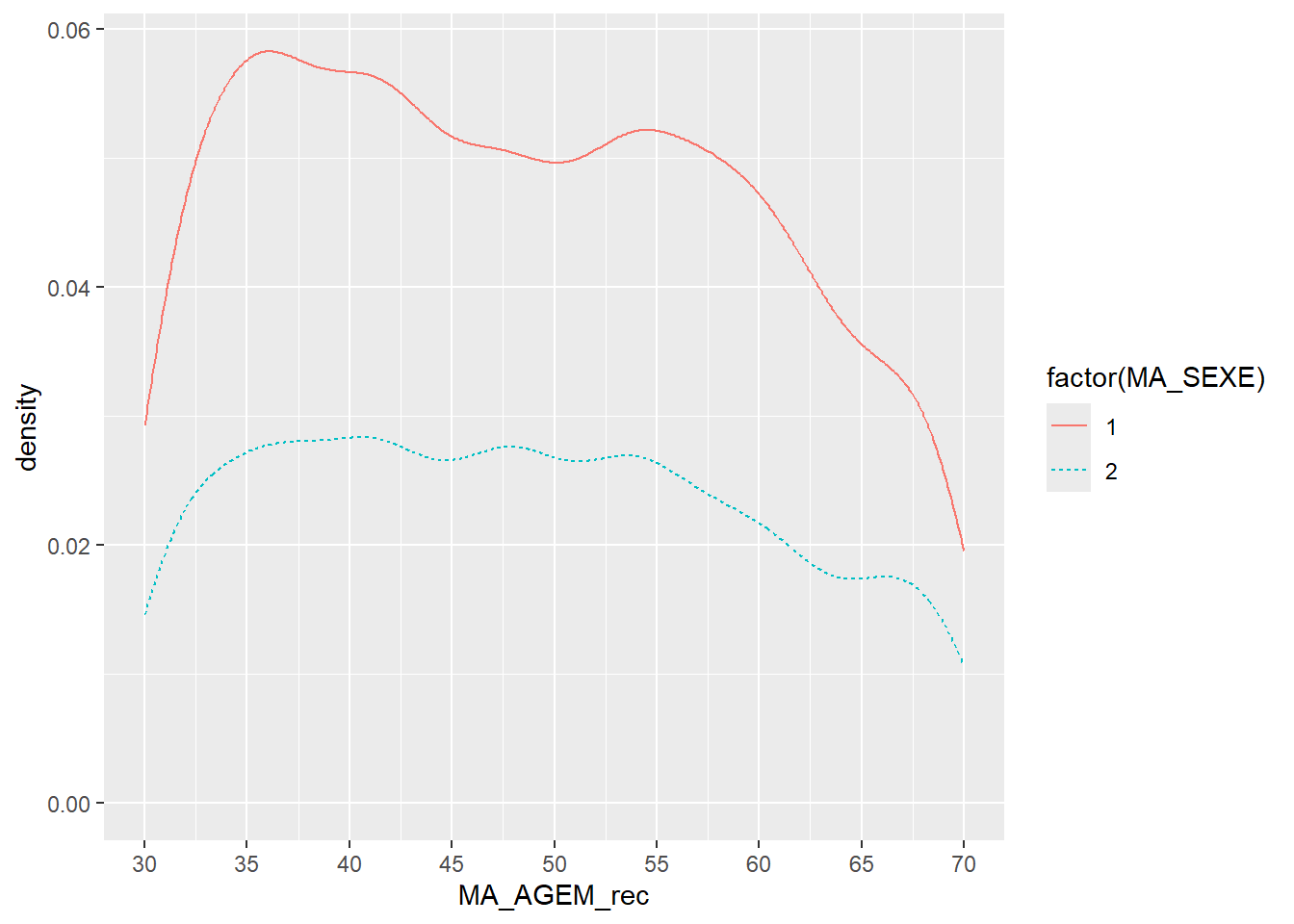
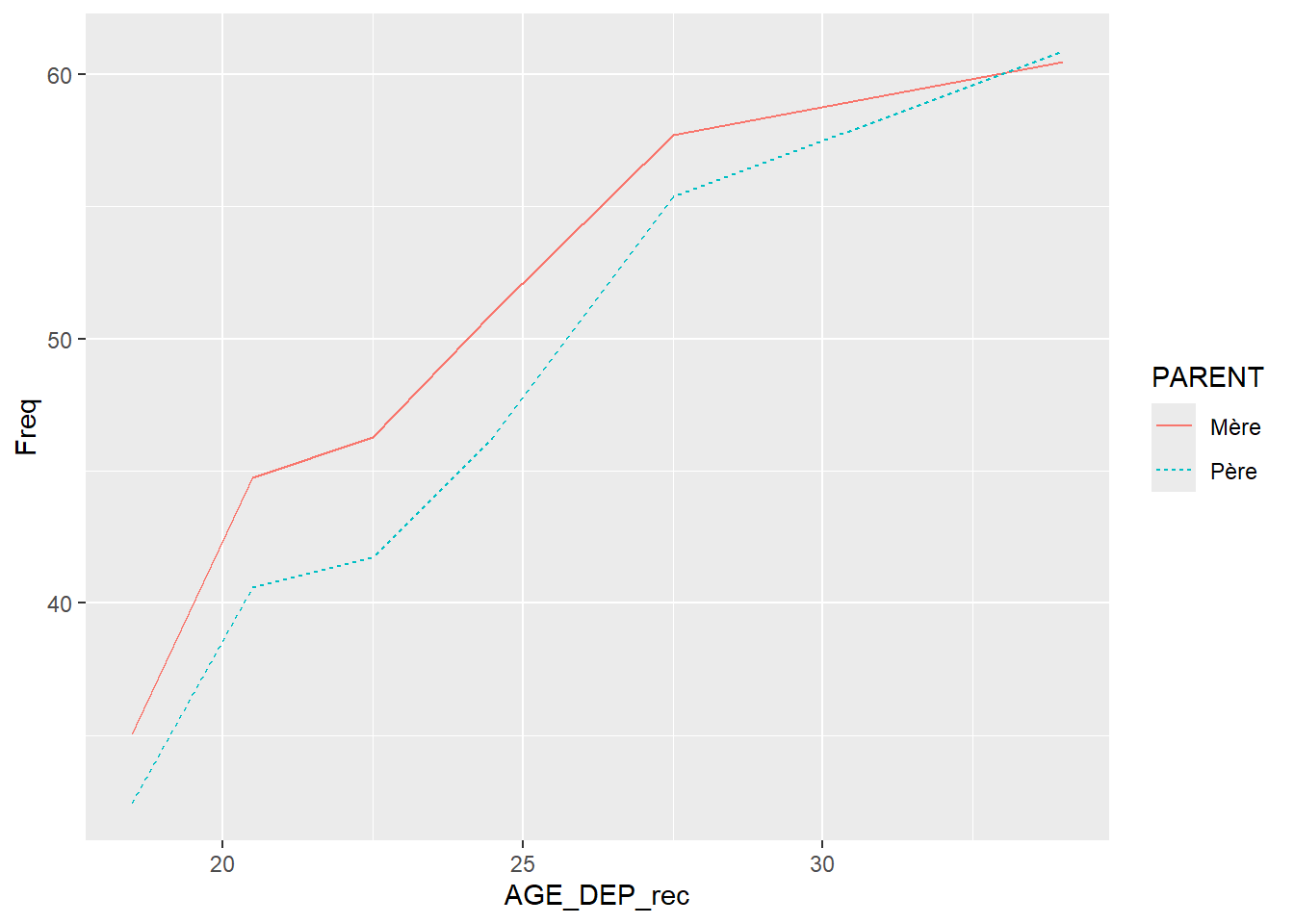
Distribution pondérée des enquêtés ERFI en fonction de l’âge (x) et du sexe (courbes lissées) en faisant varier le type des lignes en fonction de la variable Sexe (trait plein pour homme, tiret pour femme)

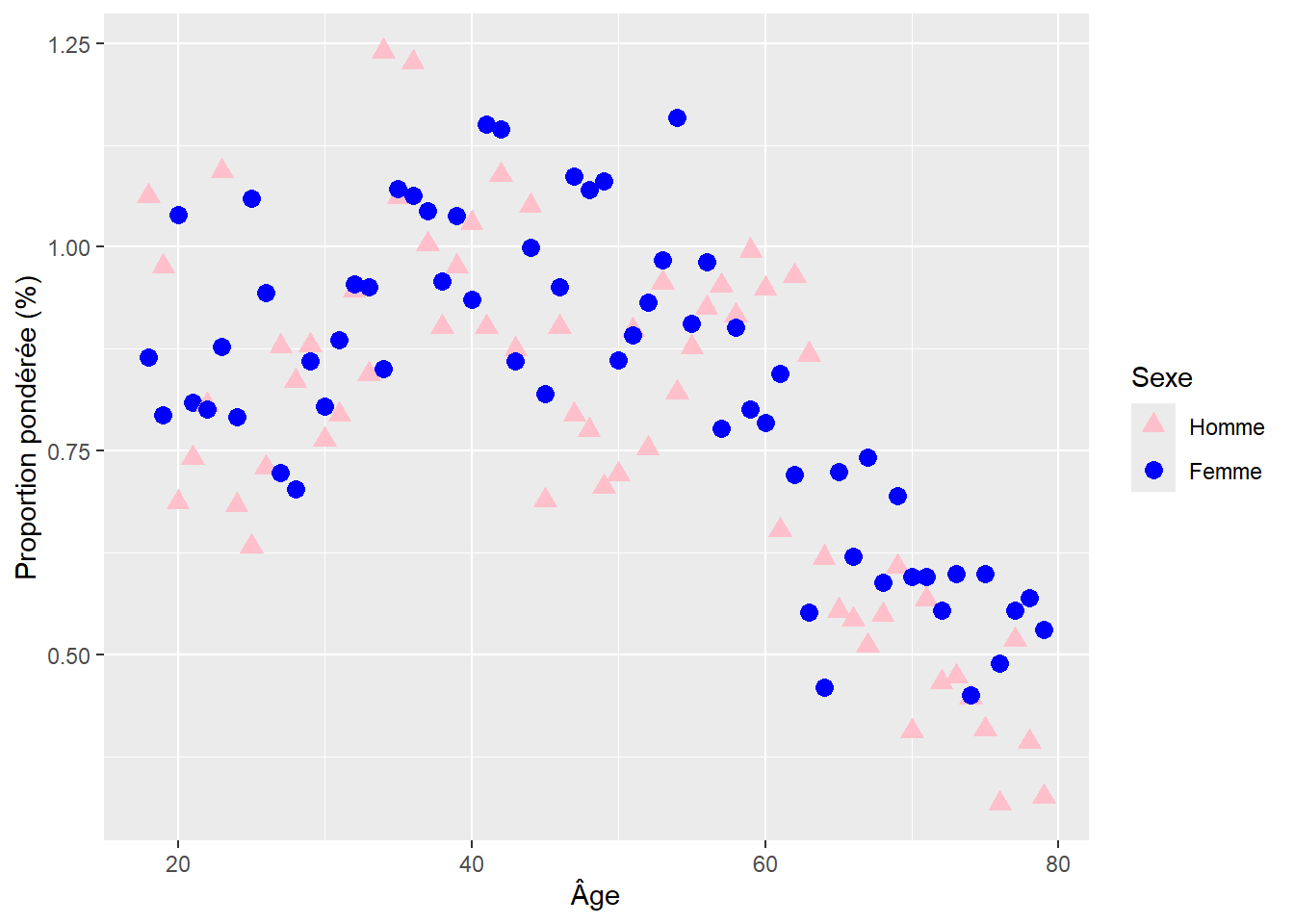
• shape : Permet de définir la forme des éléments graphiques, par exemple, pour un nuage de points. Vous pouvez choisir parmi des formes comme un cercle (code 1), un carré (code 0), ou un triangle (code 2), ce qui est utile pour distinguer les catégories. La liste des formes disponibles (et les codes correspondants) peut être consultée à cette adresse.
  

Exemple
Distribution (en %) des enquêtés selon l’âge et le sexe en faisant varier la forme en fonction de la variable Sexe (triangle rose pour homme, rond bleu pour femme)

Exemple

L’option fill permet de colorer les éléments d’un graphique en fonction des catégories ou modalités d’une variable catégorielle, facilitant ainsi la distinction visuelle des groupes.
Dans l’exemple basé sur le data.frame Opinion_PCS, fill est utilisée pour différencier les opinions (Opinion) sur la responsabilité de la prise en charge des personnes âgées à domicile, en colorant les barres selon ces opinions. L’option color, quant à elle, peut être utilisée pour attribuer une couleur spécifique aux contours des barres en fonction de ces mêmes opinions (optionnelle).

ggplot(Opinion_PCS, aes(x = PCS, y = Freq, fill = Opinion, color = Opinion))

Pour que le graphique prenne forme, il est nécessaire de spécifier le type de représentation souhaité. Cela s’effectue en ajoutant une couche géométrique à l’aide de la fonction geom.

2.3.2.2.4 Choisir le type de graphique  

Une fois les données et les variables associées aux axes X et Y, la prochaine étape consiste à ajouter une couche à notre graphique (avec le signe +) pour définir le type de graphique souhaité. 

Le type de graphique détermine la manière dont les données seront représentées visuellement. ggplot2 offre une variété de géométries (aussi appelées geom) pour chaque type de représentation graphique, en fonction de la nature des données que vous souhaitez représenter.

Les principaux exemples de geometries proposées par ggplot2 sont les suivants:

Histogramme (geom_histogram())

Boxplot (geom_boxplot())

Densité (geom_density())

Diagramme en barre (geom_bar())

Nuage de points (geom_point())

Ligne (geom_line())

On trouvera d’autres exemples de géométries (et les codes R correspondants) dans la galerie de graphes R.

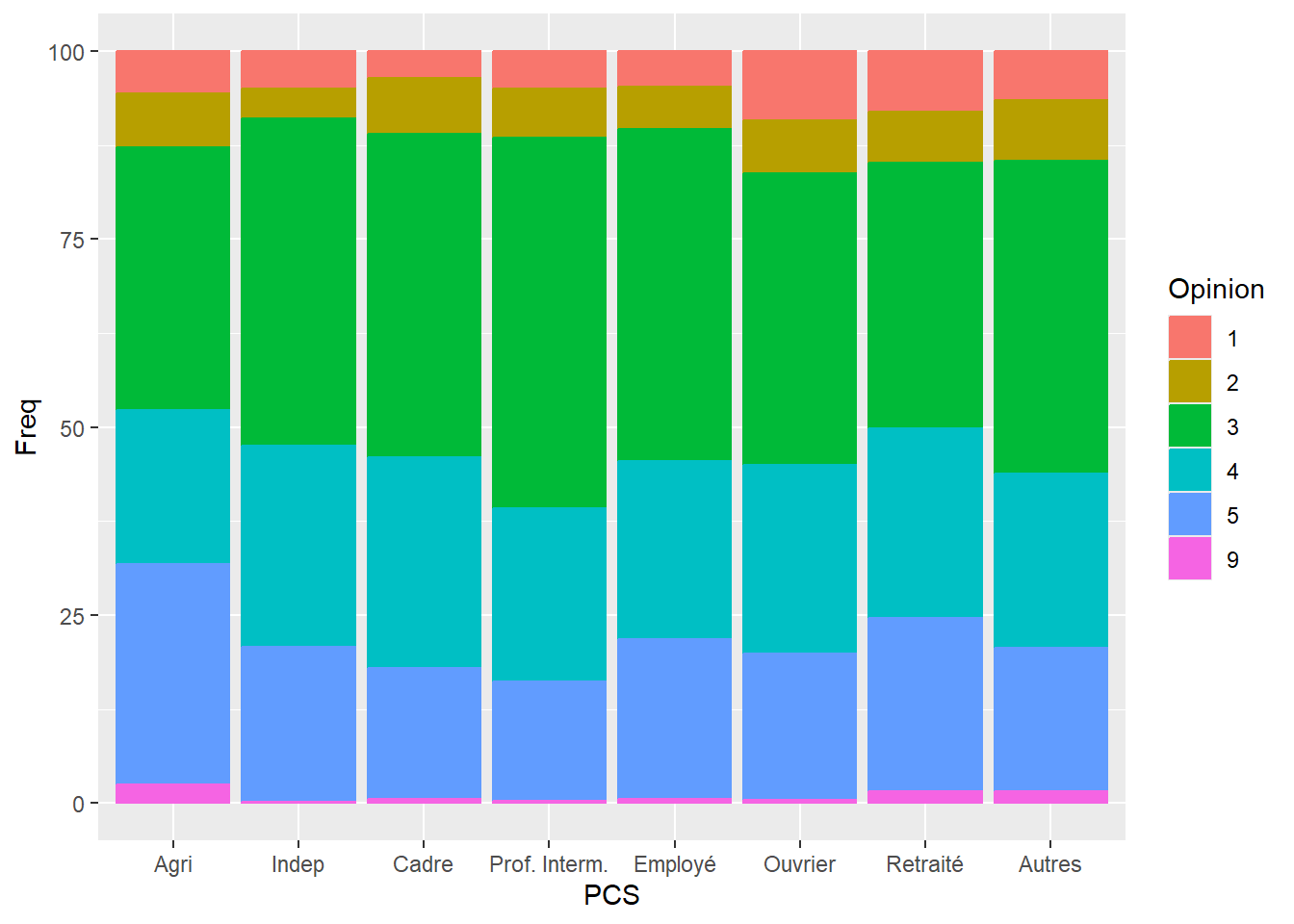
Dans l’exemple de la représentation des proportions pondérées des différentes opinions en fonction de la PCS, les deux variables d’intérêt (Opinion et PCS) sont deux variables catégorielles. La visualisation la plus appropriée pour ce type de données est un diagramme à barres. L’ajout de ce type de représentation au code s’effectue en utilisant une nouvelle couche (avec le signe +) et la fonction geom_bar() dans ggplot2.

ggplot(Opinion_PCS, aes(PCS, Freq, fill = Opinion, color = Opinion)) +
 geom_bar()

Cette instruction ne permet toujours pas d’afficher correctement le graphique car geom_bar() par défaut ne sait pas quelles statistiques doivent être utilisées pour la représentation.

2.3.2.2.5 Définir les statistiques à représenter  

Dans ggplot2, l’option stat, utilisée dans les fonctions geom(), permet de spécifier la transformation statistique que l’on souhaite appliquer aux données avant leur représentation graphique.

Chaque geom() dans ggplot2 applique par défaut une transformation statistique spécifique. Par exemple, dans le cas de geom_bar (diagramme en barres), la transformation par défaut est stat = "count", qui calcule automatiquement le nombre d’observations dans chaque catégorie d’une variable catégorielle. Ces transformations statistiques simplifient la création de graphiques de base, mais il est parfois nécessaire de les personnaliser pour répondre à des besoins spécifiques.

Si les données ont déjà été agrégées ou transformées en amont (par exemple, en calculant des proportions ou des moyennes), il est possible de désactiver toute transformation statistique supplémentaire sur les données en utilisant stat = "identity" dans la fonction geom(). Cela indique à ggplot2 que les valeurs fournies doivent être utilisées telles quelles dans le graphique.

Dans l’exemple basé sur le jeu de données Opinion_PCS, les proportions pondérées (Freq) des opinions ont été calculées au préalable. Pour représenter ces proportions directement, sans appliquer de transformation statistique aux données, il faut ainsi utiliser geom_bar() avec stat = "identity".

ggplot(Opinion_PCS, aes(PCS, Freq, fill = Opinion, color = Opinion)) +
  geom_bar(stat = "identity")

Affichage des barres côte à côte avec position = “dodge”

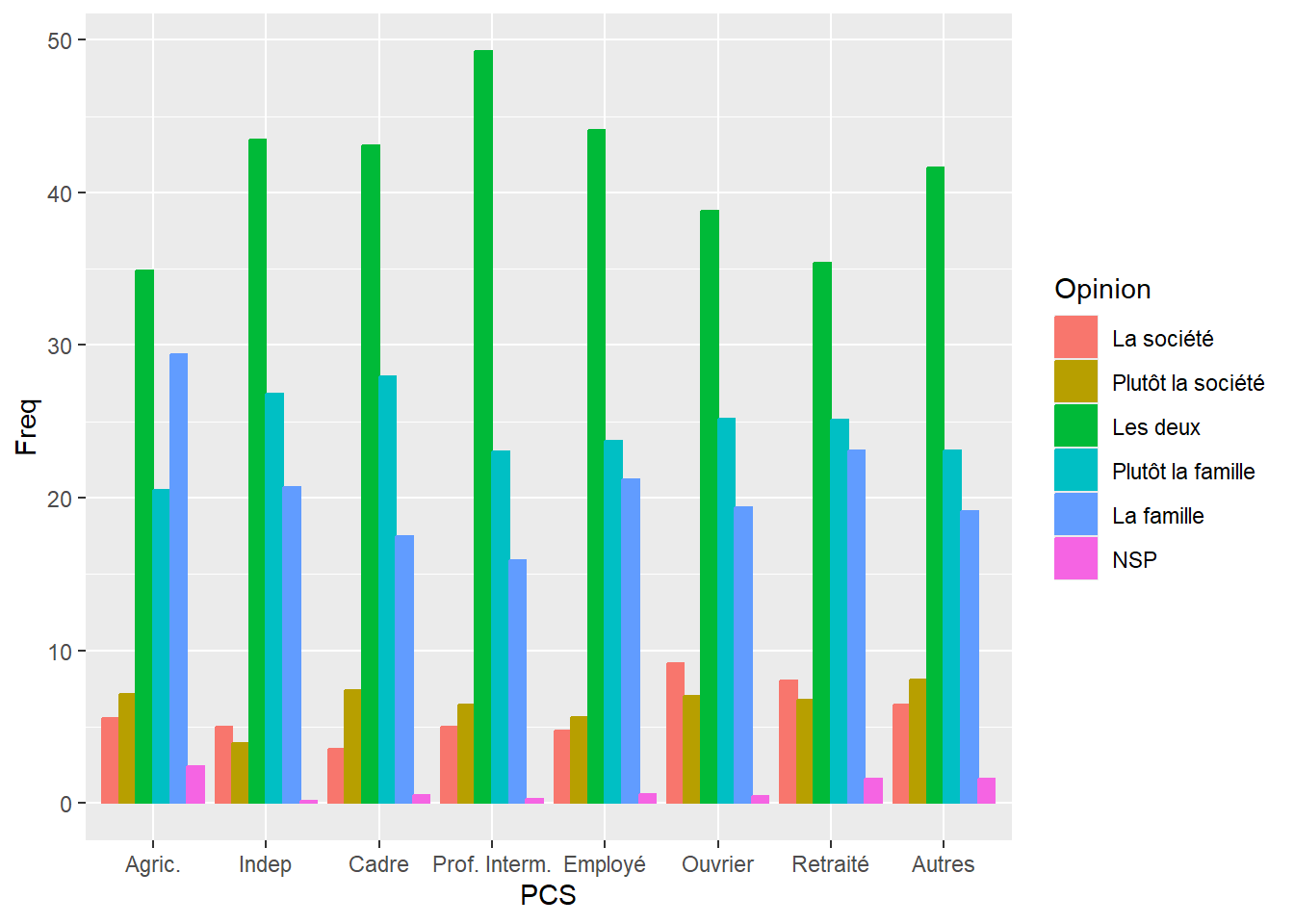
Par défaut, l’utilisation de geom_bar() produit un graphique où les barres sont empilées lorsqu’il y a plusieurs catégories pour une même valeur sur l’axe x. Si vous souhaitez comparer directement ces catégories, il est possible de les afficher côte à côte en utilisant l’argument position = "dodge". Cela permet de visualiser chaque catégorie séparément plutôt que de les empiler.

ggplot(Opinion_PCS, aes(PCS, Freq, fill = Opinion, color = Opinion)) +
  geom_bar(stat = "identity", position = "dodge")

L’argument position = "dodge" peut être utilisé dans différents types de graphiques où il est utile de comparer des sous-catégories en les affichant côte à côte (geom_boxplot par exemple).

Représentation en barres horizontales avec coord_flip()

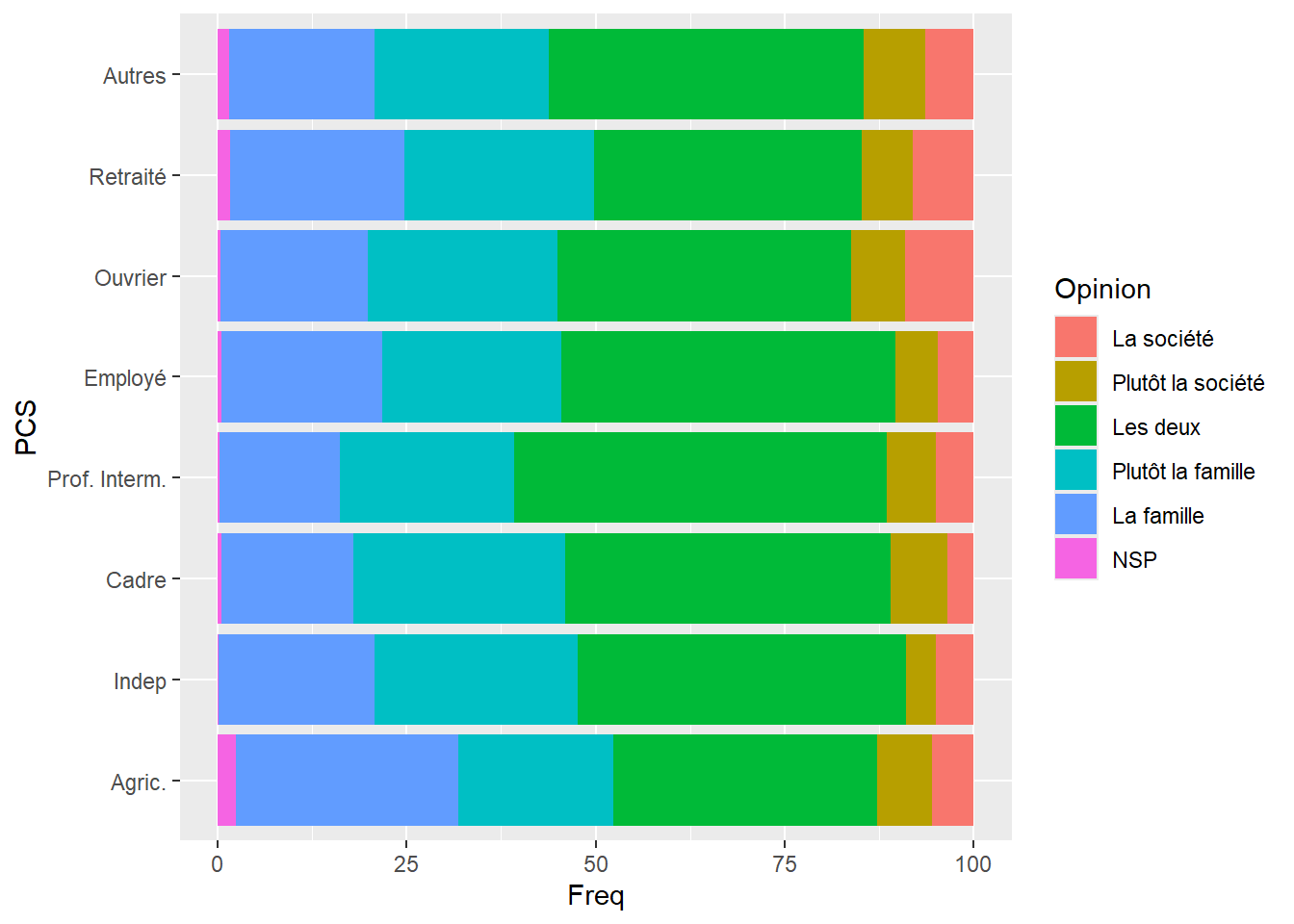
Il est possible de représenter des barres horizontales plutôt que verticales grâce à la fonction coord_flip().

ggplot(Opinion_PCS, aes(x = PCS, y = Freq, fill = Opinion)) +
  geom_bar(stat = "identity") +
    coord_flip() #Afficher des barres horizontales

Quelques exemples de transformation statistique dans ggplot2

Statistique (stat)	Description	Paramètres principaux	geom() par défaut
stat_identity()	Aucune transformation
stat_bin()	Comptage des observations	binwidth, origin	geom_bar(), geom_histogram()
stat_density()	Estimation de densité	adjust, kernel	geom_density()
stat_smooth()	Lissage (ajout d’une courbe de tendance)	method, se	geom_smooth()
stat_boxplot()	Calcul des données pour un boxplot	coef	geom_boxplot()
stat_summary()	Résumé des données avec une fonction	fun, fun.min, fun.max	geom_pointrange(), geom_errorbar()
stat_qq()	Comparaison quantile-quantile	dparams, distribution	geom_qq()
stat_sf()	Visualisation de données géographiques (sf)		geom_sf()

2.3.2.2.6 Ajuster les axes du graphique  

Les axes jouent un rôle essentiel dans la lisibilité et l’interprétation d’un graphique. ggplot2 met à disposition des outils puissants pour personnaliser divers aspects des axes, comme leur échelle, leurs graduations ou les étiquettes associées. 

L’ajout de couches au graphique à l’aide des fonctions scale_x_continuous et/ou scale_y_continuous, utilisées pour ajuster les axes associés à des variables continues, permet notamment :

• De contrôler les graduations avec breaks :  
  Cet argument permet de spécifier explicitement les positions des graduations sur l’axe. Par défaut, ggplot2 détermine automatiquement ces positions, mais elles peuvent être ajustées pour refléter des valeurs spécifiques ou améliorer la lisibilité du graphique. Par exemple, utiliser breaks = seq(a, b, c) permet de graduer l’axe entre les valeurs a et b, avec un intervalle régulier de c entre chaque graduation.
• De fixer les bornes de l’axe avec limits :  
  Cet argument permet de restreindre ou d’étendre l’affichage d’un axe à une plage définie, en fournissant un vecteur contenant deux valeurs : le minimum et le maximum. Si les limites par défaut de l’axe ne conviennent pas et que l’on souhaite restreindre l’affichage à une plage précise, on peut utiliser limits = c(a, b), où a est la borne inférieure et b la borne supérieure souhaitées.

Exemple  Distribution pondérée des enquêtés ERFI en fonction de l’âge (x) et du sexe (courbes lissées)  en graduant les axes de 20 à 75, avec un pas de 5

ggplot(ERFI1_FPA, aes(x = MA_AGEM_rec, weight = poids12, color = factor(MA_SEXE), linetype = factor(MA_SEXE))) +
  stat_density(geom = "line") +
  scale_x_continuous(breaks = seq(20, 75, 5))

Exemple
Distribution pondérée des enquêtés ERFI en fonction de l’âge (x) et du sexe (courbes lissées)
en limitant la plage d’affichage des valeurs de l’axe de 30 à 70

ggplot(ERFI1_FPA, aes(x = MA_AGEM_rec, weight = poids12, color = factor(MA_SEXE), linetype = factor(MA_SEXE))) +
  stat_density(geom = "line") +
  scale_x_continuous(breaks = seq(20, 75, 5), limits = c(30, 70)) 

Pour les axes associés à des variables catégorielles/discrètes, ggplot2 offre également les fonctions scale_x_discrete et scale_y_discrete. Ces fonctions permettent notamment de modifier le label des catégories avec labels, qui permet de spécifier un vecteur de nouvelles étiquettes pour chaque catégorie.

Lorsque l’on ne souhaite pas modifier l’ordre par défaut des catégories (alphabétique ou numérique croissant), il n’est pas nécessaire de convertir explicitement les variables catégorielles en facteur pour personnaliser les étiquettes des axes. En effet, il est possible de modifier directement les étiquettes des niveaux/modalités des variables dans l’instruction ggplot() en utilisant l’argument scale_x_discrete(labels = c()).

Exemple
Répartition des opinions relatives à la prise en charge des personnes âgées en fonction de la PCS en associant les labels de la variable PCS directement dans l’instruction ggplot() avec scale_x_discrete(labels = c())*

#Création du data.frame Opinion_PCS_ex fournissant les proportions pondérées d'opinion sur la responsabilité de prise en charge des personnes âgées en fonction de la PCS, sans l'étape de conversion de la variable PCS en facteur pour y associer des labels

Opinion_PCS_ex <- wtd.table(exemple1$AH_CS8, exemple1$VA_QPERSAGE, weights = exemple1$poids12) |> 
  lprop()
Opinion_PCS_ex <- as.data.frame(Opinion_PCS_ex) |> 
  rename(
    PCS = Var1,          # Remplacer Var1 par le nom "PCS"
    Opinion = Var2              # Remplacer Var2 par le nom "Opinion"
  ) |> 
  filter(!(Opinion == "Total" | PCS == "Ensemble"))

#Création du diagramme en barres en associant les labels des modalités de la variable PCS dans l'instruction ggplot() avec `scale_x_discrete(labels = c())

ggplot(Opinion_PCS_ex, aes(PCS, Freq, fill = Opinion, color = Opinion)) +
  geom_bar(stat = "identity") +
  scale_x_discrete(labels = c("1" = "Agri", "2" = "Indep", "3" = "Cadre", "4" = "Prof. Interm.", "5" = "Employé", "6" = "Ouvrier", "7" = "Retraité", "8" = "Autres" ))

2.3.2.2.7 Ajouter des éléments d’habillage (titre, champ, source)  

Une fois qu’un graphique est créé, il est important de l’enrichir avec des éléments d’habillage qui permettent d’en améliorer la lisibilité et la compréhension. Ces éléments incluent principalement le titre du graphique, les légendes, les labels des axes, ainsi que la source des données utilisée.

La fonction labs() permet de personnaliser les éléments textuels du graphique, tels que le titre (avec l’argument title), le sous-titre (avec subtitle), la source (avec caption) ainsi que les labels des axes (avec x et y).

Dans l’exemple tiré du data.frame Opinion_PCS, nous pouvons ajouter grâce à la couche labs():

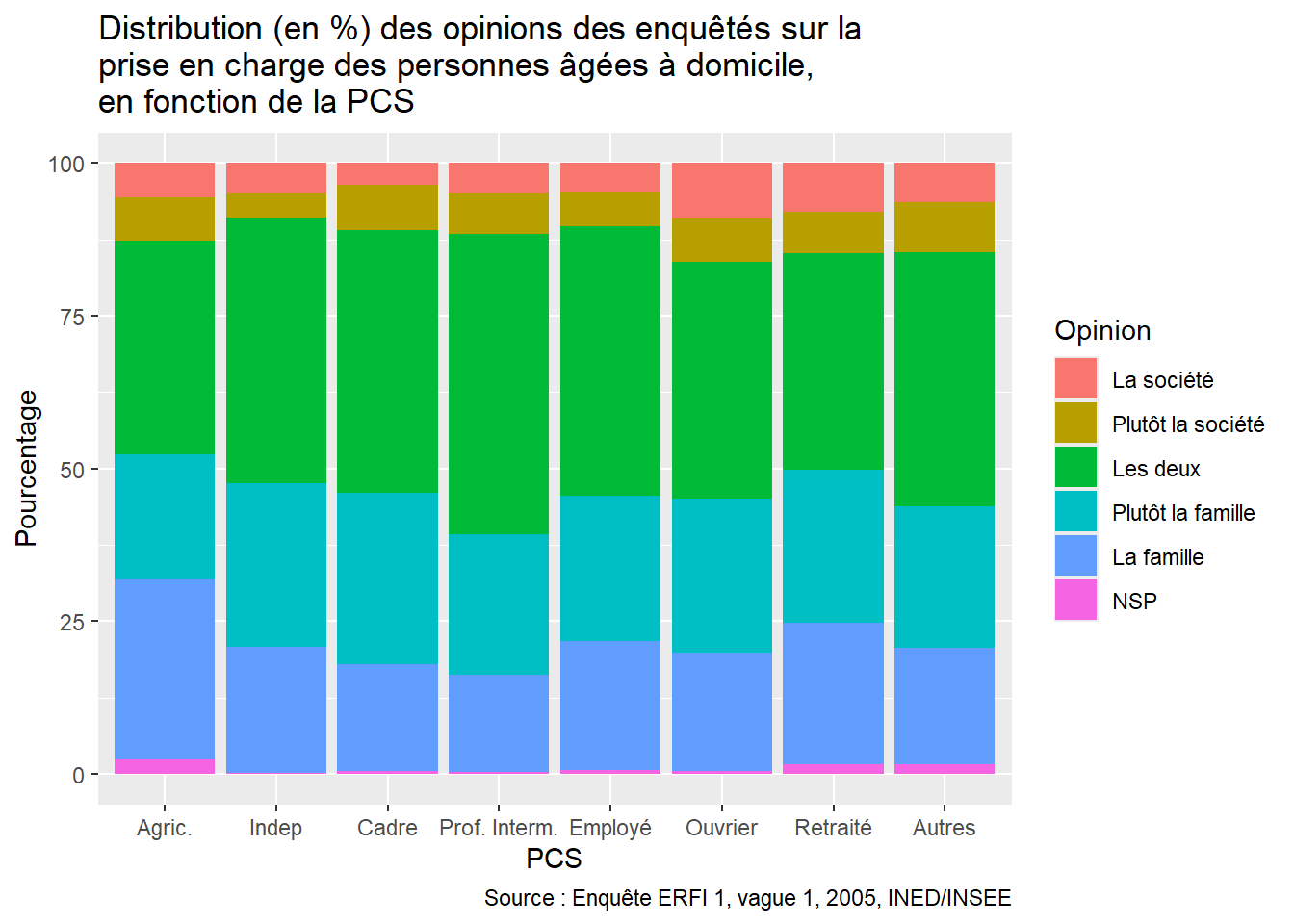
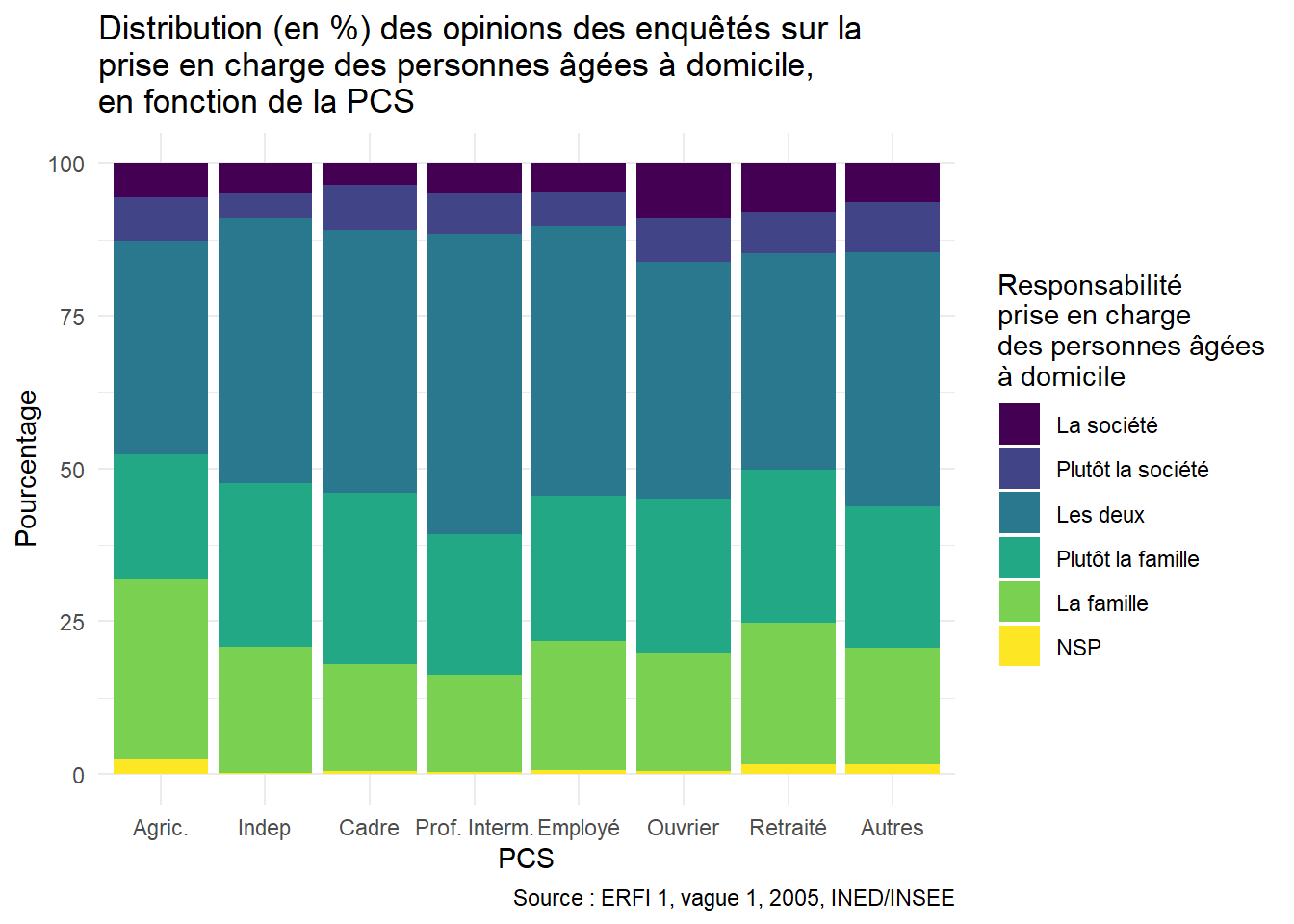
• le titre suivant : “Distribution (en %) des opinions des enquêtés sur la prise en charge des personnes âgées à domicile par la société ou la famille, en fonction de la PCS”;
• le nom des axes : x pour la PCS et y pour le pourcentage;
• la source: “Enquête Étude des relations familiales et intergénérationnelles (ERFI 1), vague 1, 2005, INED/INSEE”. 

Le code suivant permet d’ajouter ces éléments à la représentation:

ggplot(Opinion_PCS, aes(x = PCS, y = Freq, fill = Opinion)) +
  geom_bar(stat = "identity") +
  labs(
    title = "Distribution (en %) des opinions des enquêtés sur la\nprise en charge des personnes âgées à domicile,\nen fonction de la PCS", # Ajout du titre
    #Pour mettre une partie du texte à la ligne, il suffit d’introduire un `\n` dans la chaîne de caractères 
    x = "PCS", # Titre de l'axe x
    y = "Pourcentage", # Titre de l'axe y
    caption = "Source : Enquête ERFI 1, vague 1, 2005, INED/INSEE" # Source
  ) 

Astuce

Si le texte à afficher est trop long, le caractère \n permet de retourner à la ligne à l’endroit où il est placé, afin d’afficher ce texte sur deux lignes.

2.3.2.2.8 Personnaliser l’apparence du graphique (couleur, légende, thème)  

Un graphique doit être informatif, mais aussi visuellement attrayant et facile à comprendre. La personnalisation de l’apparence du graphique permet de modifier plusieurs aspects visuels, comme la couleur des éléments, l’apparence de la légende et du titre, ou encore le style global du graphique.

Personnaliser les couleurs du graphique

La couleur est un élément clé dans un graphique, car elle permet de différencier facilement les catégories ou séries de données.

Dans ggplot2, la couleur des éléments visuels (points, lignes, barres, etc.) est contrôlée par les fonctions scale, qui permettent de personnaliser l’apparence du graphique. Ces fonctions acceptent trois arguments principaux :

• name : qui définit le titre de la légende ;
• values : qui spécifie les couleurs à associer à chaque catégorie ou série (sous forme d’un vecteur contenant autant de couleurs que d’éléments à afficher) ;
• labels : qui permet de personnaliser directement les noms des catégories affichées dans la légende.
  

Pour personnaliser la couleur des éléments graphiques à l’aide de l’argument values, ggplot2 offre deux possibilités :

• Manuellement, en attribuant des couleurs spécifiques ;
• En utilisant des palettes prédéfinies pour des associations de couleurs harmonieuses.
  

Définir des couleurs manuellement

Vous pouvez définir les couleurs manuellement en utilisant :

• scale_color_manual(), pour les lignes ou les points;
• scale_fill_manual(), pour les éléments remplis, comme les barres d’un histogramme.
  

Ces fonctions permettent d’assigner des couleurs spécifiques à chaque catégorie ou modalité d’une variable.

Pour choisir ces couleurs, vous disposez de deux options :

• Utiliser les noms de couleurs reconnus par R.
  Vous pouvez consulter la liste complète des couleurs disponibles à cette adresse.
• Utiliser des codes hexadécimaux (HTML) qui démarrent toujours par l’opérateur # pour une plus grande précision.
  Pour trouver le code correspondant à une couleur précise, vous pouvez utiliser un sélecteur de couleurs tel que celui-ci.

Exemple avec scale_color_manual() et scale_fill_manual()*

Utiliser des noms de couleurs reconnus par ggplot2 :

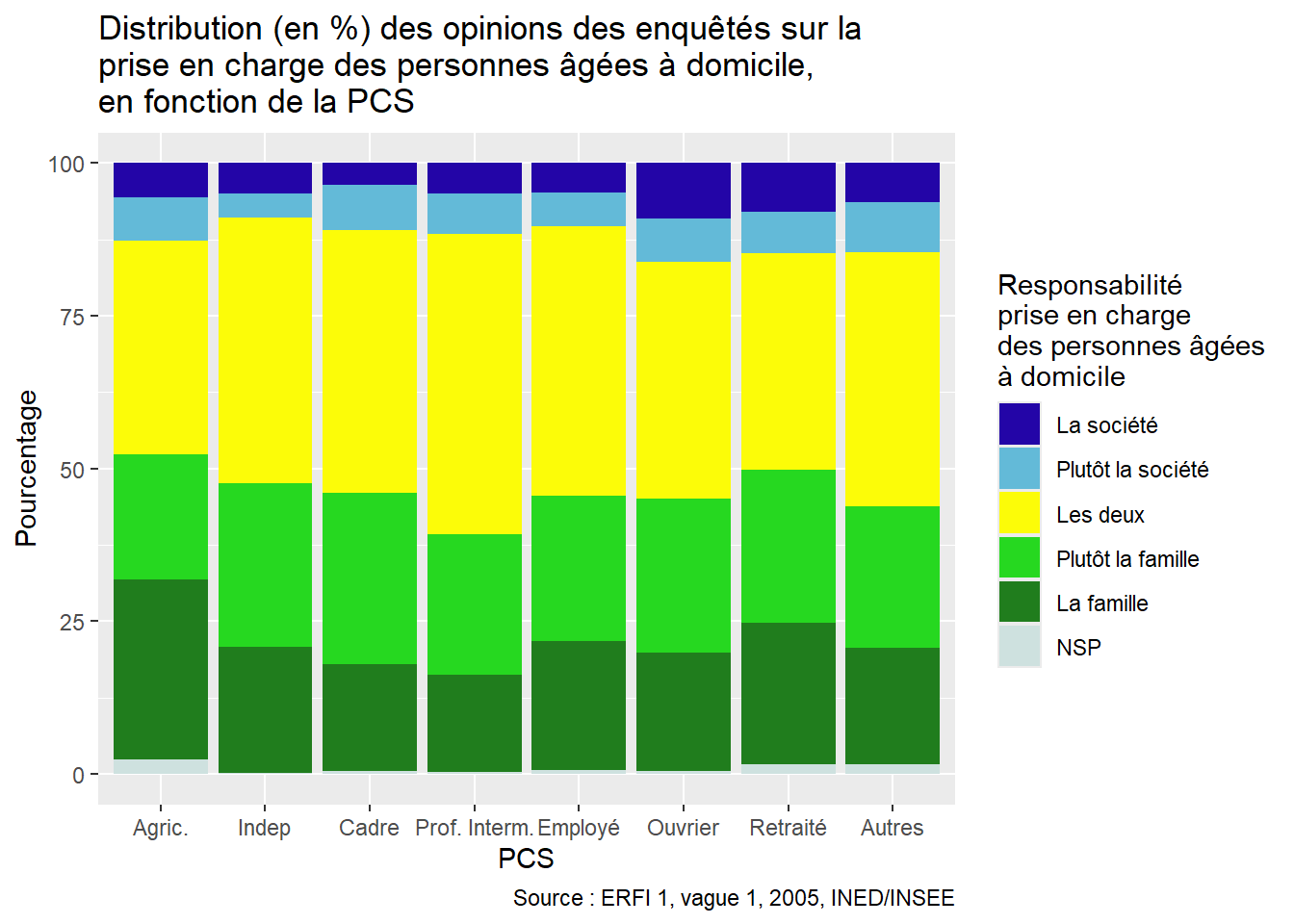
ggplot(Opinion_PCS, aes(x = PCS, y = Freq, fill = Opinion)) +
  geom_bar(stat = "identity") +
  labs(
    title = "Distribution (en %) des opinions des enquêtés sur la\nprise en charge des personnes âgées à domicile,\nen fonction de la PCS",
    x = "PCS",
    y = "Pourcentage",
    caption = "Source : ERFI 1, vague 1, 2005, INED/INSEE"
  ) +
  scale_fill_manual(
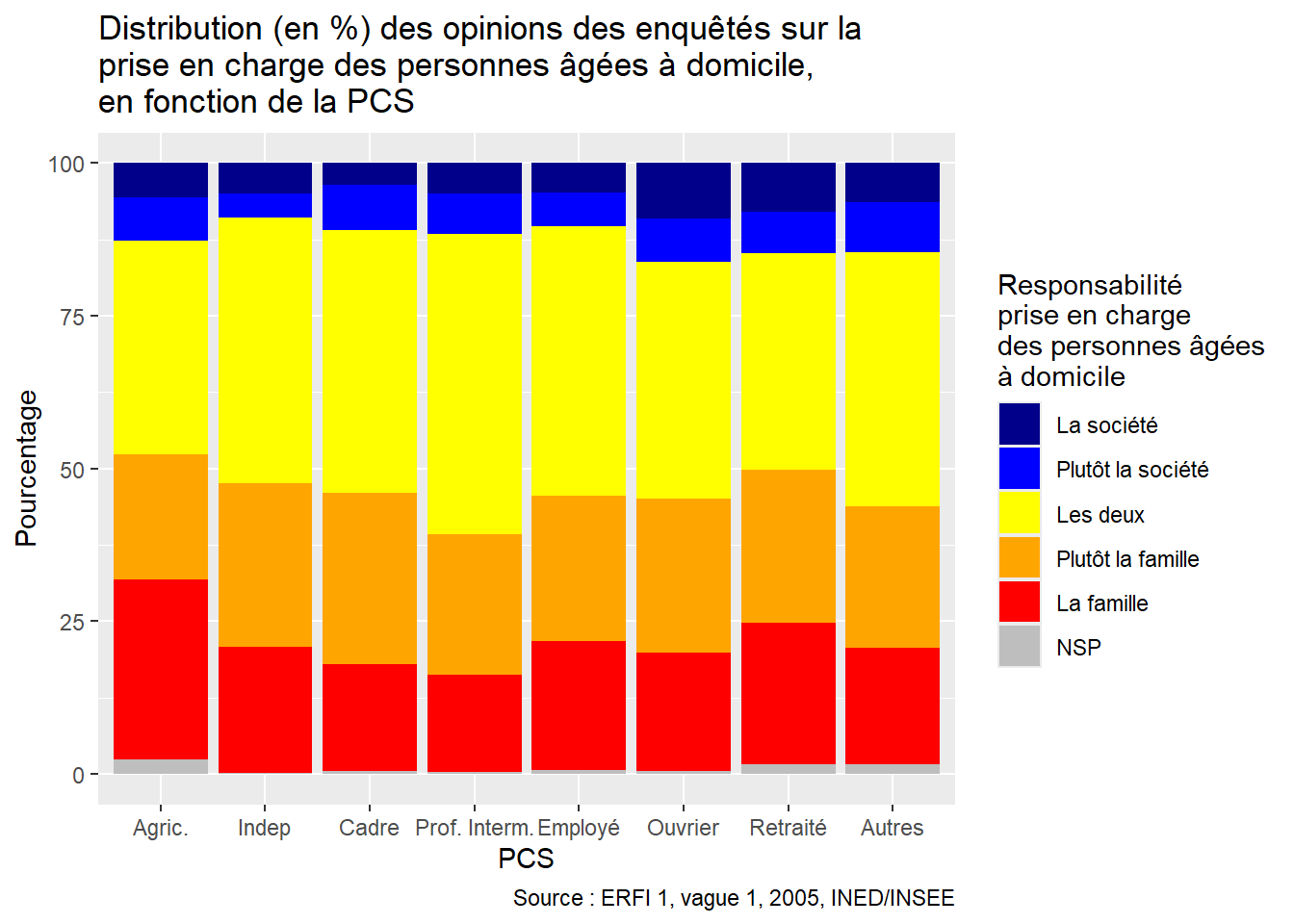
    name = "Responsabilité\nprise en charge\ndes personnes âgées\nà domicile", #Titre de la légendre
    values = c("blue4", "blue", "yellow", "orange", "red", "grey"), #Choix des couleurs
    labels = c("La société", "Plutôt la société", "Les deux", "Plutôt la famille", "La famille", "NSP")  # Associer chaque label à une couleur dans la légende
  )

Utiliser des codes hexadécimaux (HTML) :

ggplot(Opinion_PCS, aes(x = PCS, y = Freq, fill = Opinion)) +
  geom_bar(stat = "identity") +
  labs(
    title = "Distribution (en %) des opinions des enquêtés sur la\nprise en charge des personnes âgées à domicile,\nen fonction de la PCS",
    x = "PCS",
    y = "Pourcentage",
    caption = "Source : ERFI 1, vague 1, 2005, INED/INSEE") +  
scale_fill_manual(name = "Responsabilité\nprise en charge\ndes personnes âgées\nà domicile", #Titre de la légendre
                  values = c("#2305a7", "#63bad8", "#fcfc08", "#26d820", "#207d1d", "#cee1df"),  #Choix des couleurs
                  labels = c("La société", "Plutôt la société", "Les deux", "Plutôt la famille", "La famille", "NSP") # Associer chaque label à une couleur dans la légende
 )

Astuce

Il existe un grand nombre de ressources sur Internet pour choisir des couleurs et obtenir les codes hexadécimaux associés. On peut citer par exemple :

• HTML color codes : obtenir le code hexadécimal associé à n’importe quelle couleur ;
  
• W3Schools : choisir des couleurs uniques, générer des palettes, et obtenir des ressources (en anglais) sur la théorie des couleurs ;
  
• I Want hue : générer des palettes de couleurs distinctes.

Utiliser des palettes de couleurs prédéfinies

Vous pouvez également opter pour des palettes de couleurs prédéfinies, comme celles proposées par RColorBrewer, que vous pouvez explorer à cette adresse. Ces palettes peuvent être intégrées aux graphiques grâce aux fonctions scale_fill_brewer() et scale_color_brewer().

Une autre option consiste à utiliser les palettes de la famille viridis, visibles à cette adresse. Ces palettes présentent plusieurs avantages :

• Elles restent lisibles sur différents supports, y compris pour les impressions en noir et blanc,
• Elles sont conçues pour être accessibles aux personnes atteintes des formes les plus courantes de daltonisme.

Pour intégrer ces palettes, utilisez les fonctions scale_fill_viridis_d() et scale_color_viridis_d().

D’autres exemples de palettes de couleurs prédéfinies peuvent être consultés ici.

Exemple
Pour la représentation tirée du data.frame Opinion_PCS, il est possible d’utiliser différentes palettes de couleurs.

Utiliser une palette de couleurs prédéfinies basées sur RColorBrewer

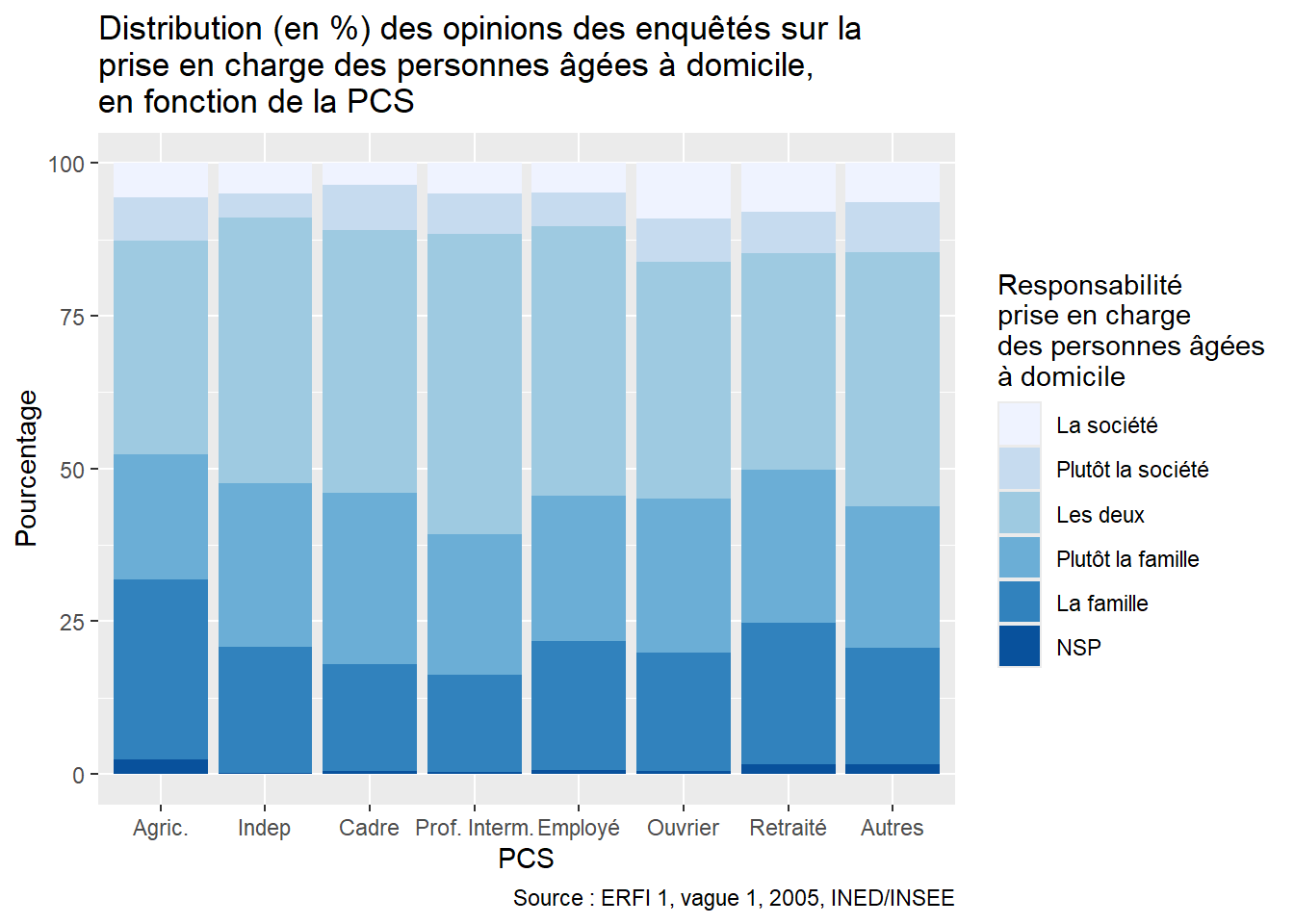
ggplot(Opinion_PCS, aes(x = PCS, y = Freq, fill = Opinion)) +
  geom_bar(stat = "identity") +
  labs(
    title = "Distribution (en %) des opinions des enquêtés sur la\nprise en charge des personnes âgées à domicile,\nen fonction de la PCS",
    x = "PCS",
    y = "Pourcentage",
    caption = "Source : ERFI 1, vague 1, 2005, INED/INSEE") + 
  scale_fill_brewer(name = "Responsabilité\nprise en charge\ndes personnes âgées\nà domicile", #Titre de la légendre
                    palette = "Blues", #Choix de la palette de couleurs prédéfinies
                    labels = c("La société", "Plutôt la société", "Les deux", "Plutôt la famille", "La famille", "NSP") # Associer chaque label à une couleur dans la légende 
  )

Utliser une palette de couleurs de la bibliothèque viridis

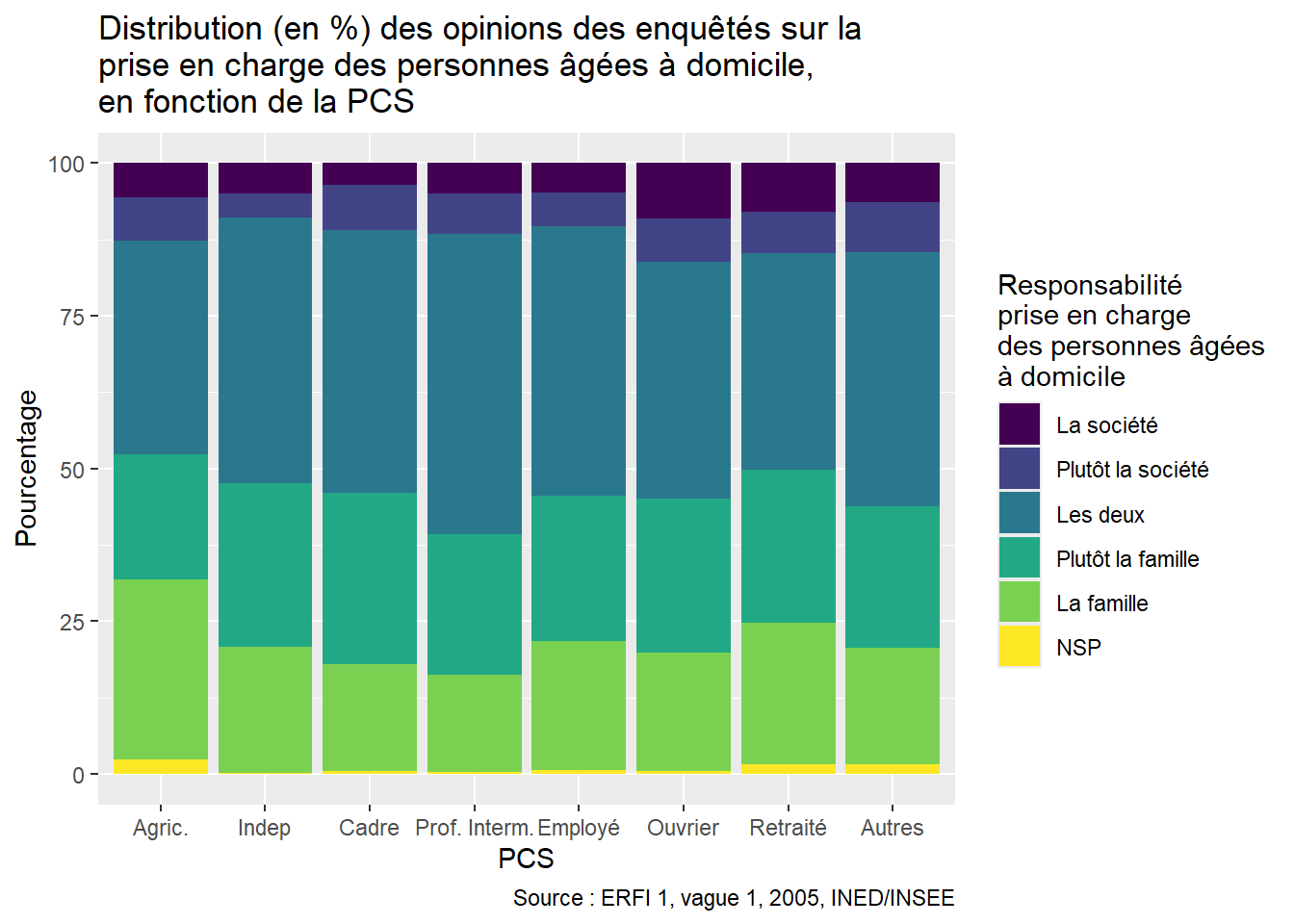
ggplot(Opinion_PCS, aes(x = PCS, y = Freq, fill = Opinion)) +
  geom_bar(stat = "identity") +
  labs(
    title = "Distribution (en %) des opinions des enquêtés sur la\nprise en charge des personnes âgées à domicile,\nen fonction de la PCS",
    x = "PCS",
    y = "Pourcentage",
    fill = "Opinion",
    caption = "Source : ERFI 1, vague 1, 2005, INED/INSEE") +
  scale_fill_viridis_d(name = "Responsabilité\nprise en charge\ndes personnes âgées\nà domicile", #Titre de la légendre
                       labels = c("La société", "Plutôt la société", "Les deux", "Plutôt la famille", "La famille", "NSP") # Associer chaque label à une couleur dans la légende) 
)

Personnaliser le type de ligne (linetype)

Dans un graphique linéaire ou de type “courbe”, le type de ligne (ou linetype) spécifié dans l’esthétique du graphique, permet de distinguer différentes séries de données.

La fonction scale_linetype_manual() permet de personnaliser le type de ligne en fonction de vos données. Vous pouvez appliquer différents types de lignes (pleine, pointillée, etc.) aux différentes séries de données pour différencier plusieurs courbes. Les codes associés aux différents types de traits qui peuvent être utilisés dans R sont répertoriés à cette adresse.

Exemple avec scale_linetype_manual() :

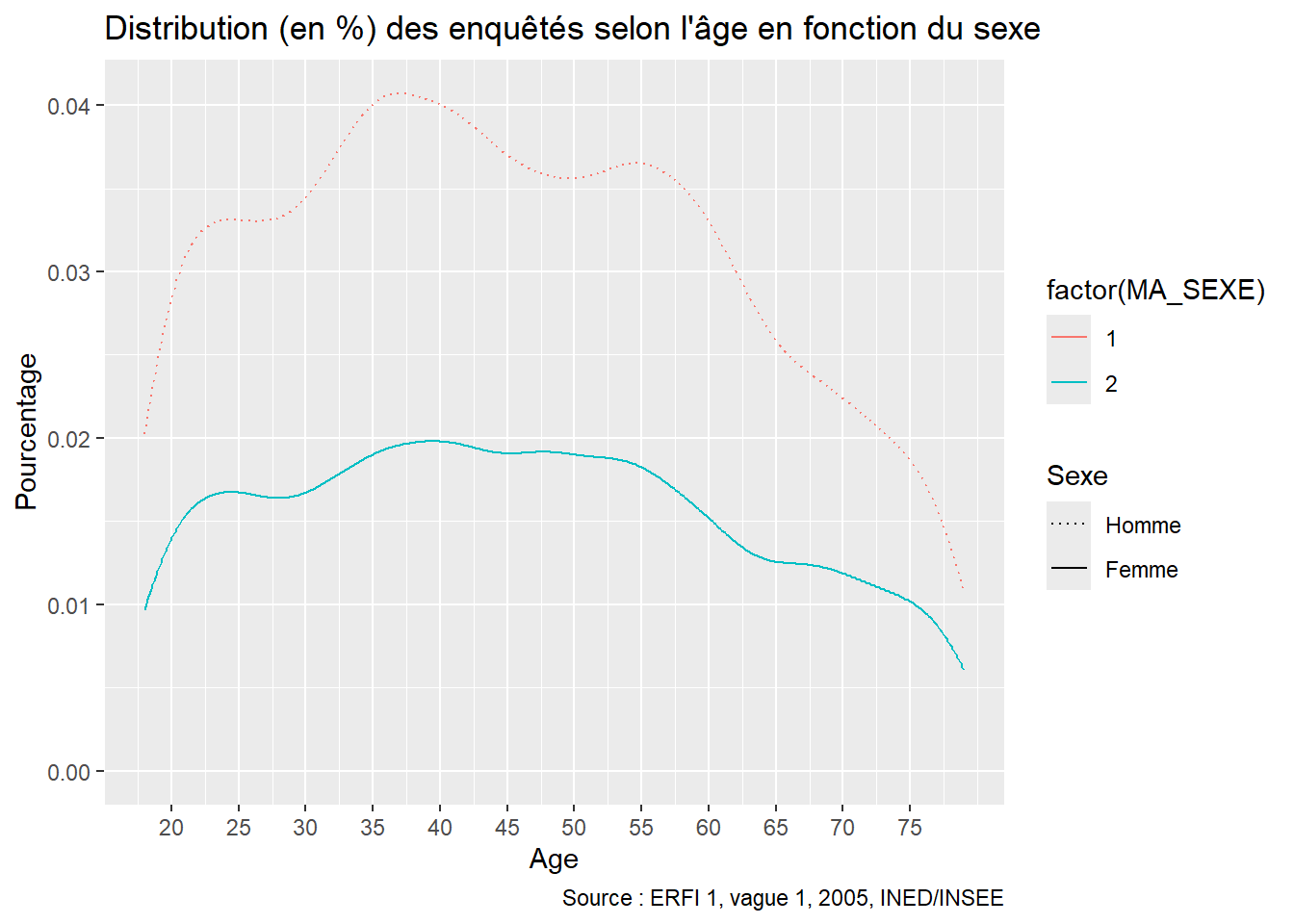
ggplot(ERFI1_FPA, aes(x = MA_AGEM_rec, weight = poids12, color = factor(MA_SEXE), linetype = factor(MA_SEXE))) +
  stat_density(geom = "line") +
  labs(
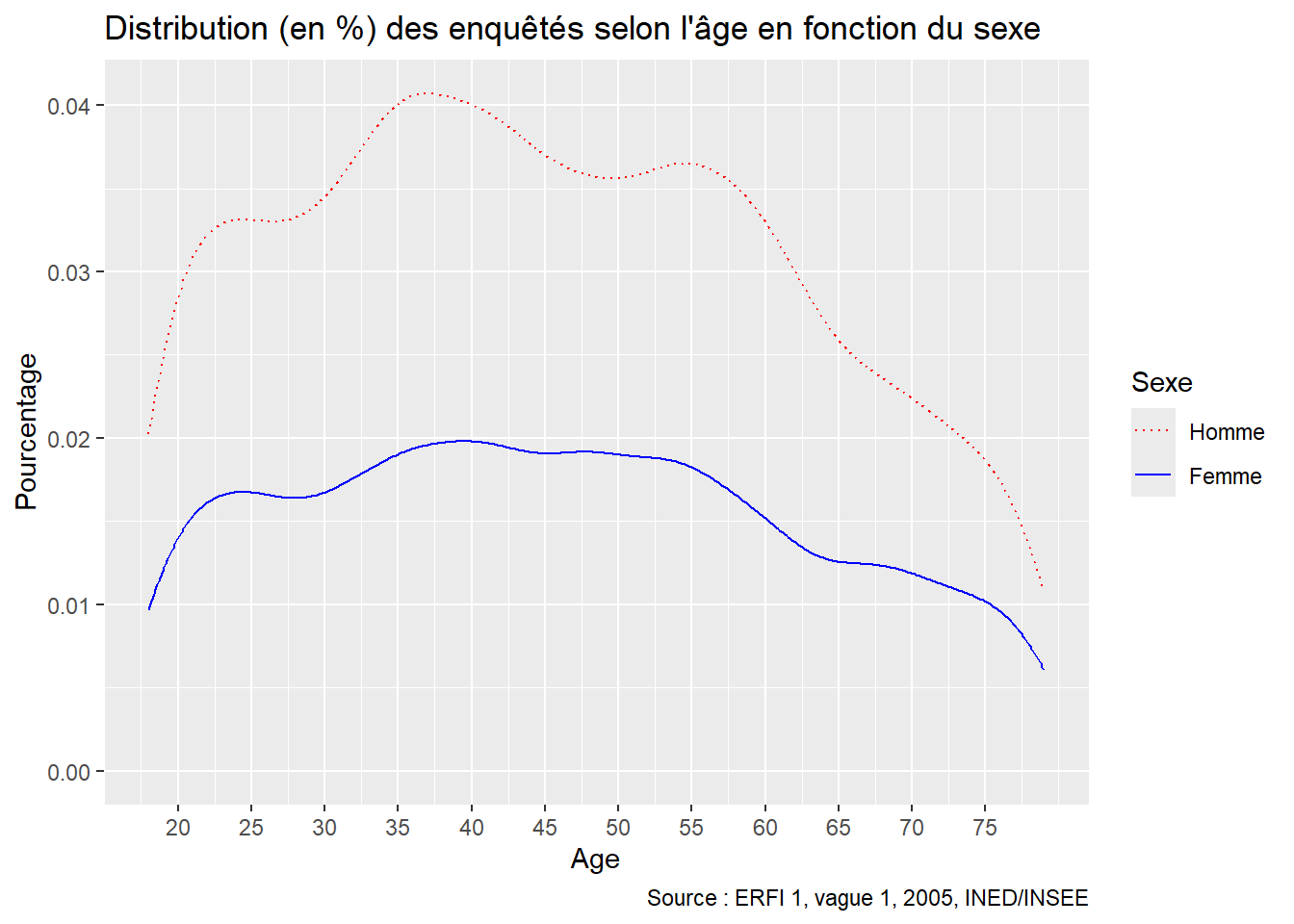
    title = "Distribution (en %) des enquêtés selon l'âge en fonction du sexe",
    x = "Age",
    y = "Pourcentage",
    caption = "Source : ERFI 1, vague 1, 2005, INED/INSEE"
  ) + 
  scale_x_continuous(breaks = seq(20, 75, 5)) +
  scale_linetype_manual(
    name = "Sexe",
    values = c(3, 1),  # Choix des types de trait pour les modalités de la variable MA_SEXE
    labels = c("Homme", "Femme")  # Labels associés aux types de ligne
  )

Actuellement, chaque esthétique (couleur et type de trait) génère une légende distincte. Pour combiner ces deux légendes en une seule, il suffit d’utiliser les mêmes titres et les mêmes entrées de légende pour les fonctions scale_linetype_manual et scale_color_manual. Cela permet d’harmoniser les légendes en les associant sous un même intitulé et avec des libellés identiques.

ggplot(ERFI1_FPA, aes(x = MA_AGEM_rec, weight = poids12, color = factor(MA_SEXE), linetype = factor(MA_SEXE))) +
  stat_density(geom = "line") +
  labs(
    title = "Distribution (en %) des enquêtés selon l'âge en fonction du sexe",
    x = "Age",
    y = "Pourcentage",
    caption = "Source : ERFI 1, vague 1, 2005, INED/INSEE"
  ) + 
  scale_x_continuous(breaks = seq(20, 75, 5)) +
  scale_color_manual(
    name = "Sexe",
    values = c("red", "blue"),  # Choix des couleurs de trait
    labels = c("Homme", "Femme") # Labels associés aux couleurs
  ) + 
  scale_linetype_manual(
    name = "Sexe",
    values = c(3, 1),  # Choix des types de trait
    labels = c("Homme", "Femme")  # Labels associés aux types de ligne
  )

Personnaliser le thème du graphique

Le thème définit l’apparence générale du graphique. ggplot2 propose des thèmes prédéfinis, mais vous pouvez aussi personnaliser le thème à l’aide de la fonction theme() pour ajuster des éléments comme le titre, les axes, la légende, et le fond du graphique.

Choisir un thème prédéfini

ggplot propose plusieurs thèmes prédéfinis qui modifient l’apparence générale de vos graphiques. Parmi ceux-ci, vous pouvez utiliser theme_minimal(), theme_light(), et d’autres pour obtenir un style plus épuré ou plus détaillé selon vos besoins. Un aperçu de ces thèmes est disponible à cette adresse.
En outre, le package ggthemes élargit encore les options en proposant des thèmes supplémentaires, y compris certains qui imitent la mise en forme des graphiques réalisés sous d’autres logiciels comme Excel ou Stata. Vous pouvez consulter la liste complète des thèmes proposés par ggthemes ici.

Pour la représentation graphique issue du data.frame Opinion_PCS, nous nous contenterons d’utiliser un thème prédéfini avec theme_minimal().

ggplot(Opinion_PCS, aes(x = PCS, y = Freq, fill = Opinion)) +
  geom_bar(stat = "identity") +
  labs(
    title = "Distribution (en %) des opinions des enquêtés sur la\nprise en charge des personnes âgées à domicile,\nen fonction de la PCS",
    x = "PCS",
    y = "Pourcentage",
    fill = "Opinion",
    caption = "Source : ERFI 1, vague 1, 2005, INED/INSEE"
  ) +
  scale_fill_viridis_d(
    name = "Responsabilité\nprise en charge\ndes personnes âgées\nà domicile",
    labels = c("La société", "Plutôt la société", "Les deux", "Plutôt la famille", "La famille", "NSP")
  ) +
  theme_minimal()

Personnaliser le thème avec theme()

La fonction theme() offre une grande flexibilité pour personnaliser divers éléments du graphique, tels que les titres, les axes, les étiquettes, ou encore le texte. En modifiant les propriétés à l’intérieur de theme(), vous pouvez adapter votre graphique à vos besoins. Voici quelques exemples d’utilisation courante :

• Mettre le titre en gras
  Utilisez plot.title = element_text(face = "bold") pour appliquer un style en gras au titre du graphique.
  
• Aligner les titres des axes
  Pour aligner le titre de l’axe des abscisses à droite, ajoutez : axis.title.x = element_text(hjust = 1). Le paramètre hjust contrôle l’alignement horizontal, avec des valeurs comprises de 0 (aligné à gauche) à 1 (aligné à droite). De manière similaire, pour l’axe des ordonnées, utilisez axis.title.y = element_text(hjust = 1). Pour l’alignement vertical, on utilise l’argument vjust.
  
• Modifier le style de la légende ou du texte descriptif
  Pour aligner le champ de la source et réduire la taille de police de la légende, utilisez : plot.caption = element_text(hjust = 0, size = 8). Ici, hjust permet d’aligner le texte à gauche, et size ajuste la taille de la police.
  
• Faire pivoter les étiquettes des axes
  Si vous avez besoin de faire pivoter les étiquettes des axes, par exemple pour des étiquettes longues, utilisez : axis.text.x = element_text(angle = 45, hjust = 1). L’argument angle définit l’angle de rotation (en degrés). Dans cet exemple, les étiquettes de l’axe des x seront inclinées à 45°. 

La liste complète des options de personnalisation disponibles pour un thème peut être consultée à cette adresse.

Exemple

ggplot(Opinion_PCS, aes(x = PCS, y = Freq, fill = Opinion)) +
  geom_bar(stat = "identity") +
  labs(
    title = "Distribution (en %) des opinions des enquêtés sur la\nprise en charge des personnes âgées à domicile,\nen fonction de la PCS",
    x = "PCS",
    y = "Pourcentage",
    fill = "Opinion",
    caption = "Source : ERFI 1, vague 1, 2005, INED/INSEE"
  ) +
  scale_fill_viridis_d(
    name = "Responsabilité\nprise en charge\ndes personnes âgées\nà domicile",
    labels = c("La société", "Plutôt la société", "Les deux", "Plutôt la famille", "La famille", "NSP")
  ) +
  theme_minimal() +
  theme(
    plot.title = element_text(face = "bold"),        # Mettre le titre en gras
    axis.title.x = element_text(hjust = 1),          # Aligner le titre de l'axe x à droite
    axis.title.y = element_text(hjust = 1),          # Aligner le titre de l'axe y à droite
    axis.text.x = element_text(angle = 45, hjust = 1), # Incliner les étiquettes de l'axe x à 45°
    plot.caption = element_text(hjust = 0, size = 8) # Aligner la source à gauche et réduire la taille de police
  )

Ajouter les valeurs en % à l’intérieur du graphique avec geom_text()

La fonction geom_text() permet d’ajouter des valeurs numériques (comme des pourcentages) au-dessus ou à l’intérieur des barres empilées pour une lecture plus facile des données. Elle contient plusieurs arguments:

• aes(label = ...) : L’argument label dans aes() précise les valeurs à afficher. Dans notre exemple, la variable Freq contient les valeurs de pourcentage. Pour une plus grande lisibilité, il est préférable d’arrondir ces pourcentages grâce à la fonction round() (aes(label = round(Freq)).
  
• position_stack() : Lors de l’utilisation de geom_bar() avec stat = "identity", les segments des barres sont empilés (stacked). On utilise donc position_stack() pour positionner le texte au centre de chaque segment empilé. L’option vjust dans position_stack permet de régler la position verticale du texte. Pour centrer verticalement le texte dans chaque segment de la barre, afin qu’il soit clairement visible pour chaque catégorie on utilise vjust=0.5.
  
• color = … : Il est possible de choisir la couleur du texte affiché. On utilisera ici color = "white" pour un meilleur contraste avec les barres colorées. - size = … : L’option size permet de contrôler la taille du texte. On choisira ici size = 3.

Le code complet et son résultat graphique intégrant les valeurs de pourcentage centrées dans chaque segment de couleur figurent ci-dessous :

ggplot(Opinion_PCS, aes(x = PCS, y = Freq, fill = Opinion)) +
  geom_bar(stat = "identity") +
  labs(
    title = "Distribution (en %) des opinions des enquêtés sur la\nprise en charge des personnes âgées à domicile,\nen fonction de la PCS",
    x = "PCS",
    y = "Pourcentage",
    fill = "Opinion",
    caption = "Source : ERFI 1, vague 1, 2005, INED/INSEE"
  ) +
  scale_fill_viridis_d(
    name = "Responsabilité\nprise en charge\ndes personnes âgées\nà domicile",
    labels = c("La société", "Plutôt la société", "Les deux", "Plutôt la famille", "La famille", "NSP")
  ) +
  theme_minimal() +
  theme(
    plot.title = element_text(face = "bold"),        # Mettre le titre en gras
    axis.title.x = element_text(hjust = 1),          # Aligner le titre de l'axe x à droite
    axis.title.y = element_text(hjust = 1),          # Aligner le titre de l'axe y à droite
    axis.text.x = element_text(angle = 45, hjust = 1), # Incliner les étiquettes de l'axe x à 45°
    plot.caption = element_text(hjust = 0, size = 8) # Aligner la source à gauche et réduire la taille de police
  ) +
  geom_text(aes(label = round(Freq)), 
            position = position_stack(vjust = 0.5), 
            color = "white", size = 3) 

2.3.2.2.9 Comparer des sous-groupes à l’aide de facettes  

Les facettes sont une fonctionnalité de ggplot2 qui permettent de diviser un graphique en plusieurs sous-graphiques, chacun correspondant à un sous-groupe de données. Cette méthode est particulièrement utile pour comparer les tendances ou distributions entre des sous-groupes, ou pour observer les différences entre les niveaux ou modalités d’une ou plusieurs variables catégorielles.

Dans ggplot2, deux principales fonctions sont utilisées pour créer des facettes :

• facet_wrap()
  Cette fonction crée une série de sous-graphiques pour chaque niveau d’une seule variable. Les sous-graphiques sont organisés automatiquement en lignes et colonnes pour s’adapter à l’espace disponible. C’est une solution flexible et rapide pour explorer une seule variable catégorielle.
  
• facet_grid()
  Cette fonction génère une grille de facettes en fonction de deux variables. Les facettes sont structurées avec une variable assignée aux lignes et une autre aux colonnes. Elle est particulièrement adaptée lorsque vous souhaitez une disposition stricte et organisée pour analyser les interactions entre deux variables.
  

Fonction	Nombre de variables	Disposition	Cas d’usage
facet_wrap	Une seule variable	Grille flexible	Pour des facettes organisées sur plusieurs lignes
facet_grid	Deux variables	Grille stricte	Comparer chaque combinaison de deux variables

Exemple

Utiliser facet_wrap() pour examiner la distribution (en %) des opinions des enquêtés sur la prise en charge des personnes âgées à domicile, par sexe et en fonction de la PCS.

Dans cet exemple, basé sur le jeu de données Opinion_PCS, nous visualisons la distribution des opinions sur la prise en charge des personnes âgées (VA_QPERSAGE) selon la catégorie socioprofessionnelle (AH_CS8) et le sexe (MA_SEXE). Avant de tracer ces graphiques, il est nécessaire de recalculer les proportions en fonction des deux variables. 

Préparation des données

# Sélection et nettoyage des données
exemple1 <- select(ERFI1_FPA, VA_QPERSAGE, AH_CS8, MA_SEXE, poids12) |>             
  filter(AH_CS8 != "9")  # Supprimer les observations avec la modalité AH_CS8 = "9"

# Création des tableaux croisés pondérés par sexe
#Pour les hommes
Homme <- filter(exemple1, MA_SEXE == "1")  #Sélection des hommes (MA_SEXE == "1")
Homme_Opinion_PCS <- wtd.table(Homme$AH_CS8, Homme$VA_QPERSAGE, weights = Homme$poids12) |>  
  lprop() |>  #Calcul des pourcentages pondérés des opinions en fonction de la PCS
  as.data.frame() |> #Transformation en data.frame 
  rename(PCS = Var1, Opinion = Var2) |>  #Renommer les variables
  filter(!(Opinion == "Total" | PCS == "Ensemble")) |> #Supprimer les modalités inutiles pour la représentation
  mutate(Sexe = 1) #Création d'une nouvelle variable Sexe pour distinguer les hommes (1) et les femmes (2)

#Pour les femmes
Femme <- filter(exemple1, MA_SEXE == "2")  #Sélection des femmes (MA_SEXE == "2")
Femme_Opinion_PCS <- wtd.table(Femme$AH_CS8, Femme$VA_QPERSAGE, weights = Femme$poids12) |>  
  lprop() |>  #Calcul des pourcentages pondérés des opinions en fonction de la PCS
  as.data.frame() |>  #Transformation en data.frame 
  rename(PCS = Var1, Opinion = Var2) |>  #Renommer les variables
  filter(!(Opinion == "Total" | PCS == "Ensemble")) |>  #Supprimer les modalités inutiles pour la représentation
  mutate(Sexe = 2) #Création d'une nouvelle variable Sexe pour distinguer les hommes (1) et les femmes (2)

# Fusion des données homme et femme
Sexe_Opinion_PCS <- bind_rows(Homme_Opinion_PCS, Femme_Opinion_PCS)

# Renommer et ordonner les modalités des facteurs
Sexe_Opinion_PCS$Sexe <- factor(Sexe_Opinion_PCS$Sexe, levels = c(1, 2), labels = c("Homme", "Femme"))
Sexe_Opinion_PCS$Opinion <- factor(Sexe_Opinion_PCS$Opinion, levels = c(1, 2, 3, 4, 5, 9), 
                                   labels = c("La société", "Plutôt la société", "Les deux", 
                                              "Plutôt la famille", "La famille", "NSP"))
Sexe_Opinion_PCS$PCS <- factor(Sexe_Opinion_PCS$PCS, levels = c(1, 2, 3, 4, 5, 6, 7, 8), 
                               labels = c("Agric.", "Indép.", "Cadre", "Prof. Interm.", 
                                          "Employé", "Ouvrier", "Retraité", "Autres"))

Avertissement

Il est important de renommer Var1 et Var2 de la même manière dans Homme et Femme en vue de la fusion de ces deux tables par la suite. N’oubliez pas que R est sensible à la casse.

Utilisation de facet_wrap() pour analyser la distribution par sexe (une facette pour chaque sexe)

ggplot(Sexe_Opinion_PCS, aes(x = PCS, y = Freq, fill = Opinion)) +
  geom_bar(stat = "identity") +
  labs(
    title = "Distribution (en %) des opinions des enquêtés sur la\nprise en charge des personnes âgées à domicile,\nen fonction de la PCS",
    x = "PCS",
    y = "Pourcentage",
    fill = "Opinion",
    caption = "Source : ERFI 1, vague 1, 2005, INED/INSEE"
  ) +
  scale_fill_viridis_d(
    name = "Responsabilité\nprise en charge\ndes personnes âgées\nà domicile",
    labels = c("La société", "Plutôt la société", "Les deux", "Plutôt la famille", "La famille", "NSP")
  ) +
  theme_minimal() +
  theme(
    plot.title = element_text(face = "bold"),        # Mettre le titre en gras
    axis.title.x = element_text(hjust = 1),          # Aligner le titre de l'axe x à droite
    axis.title.y = element_text(hjust = 1),          # Aligner le titre de l'axe y à droite
    axis.text.x = element_text(angle = 45, hjust = 1), # Incliner les étiquettes de l'axe x à 45°
    plot.caption = element_text(hjust = 0, size = 8)  # Aligner la source à gauche et réduire la taille de police
  ) +
  facet_wrap(~ Sexe)  # Une facette par sexe

Utilisation de facet_grid() pour examiner la distribution selon chaque combinaison de PCS et sexe

ggplot(Sexe_Opinion_PCS, aes(x = PCS, y = Freq, fill = Opinion)) +
  geom_bar(stat = "identity") +
  labs(
    title = "Distribution (en %) des opinions des enquêtés sur la\nprise en charge des personnes âgées à domicile,\nen fonction de la PCS",
    x = "PCS",
    y = "Pourcentage",
    fill = "Opinion",
    caption = "Source : ERFI 1, vague 1, 2005, INED/INSEE"
  ) +
  scale_fill_viridis_d(
    name = "Responsabilité\nprise en charge\ndes personnes âgées\nà domicile",
    labels = c("La société", "Plutôt la société", "Les deux", "Plutôt la famille", "La famille", "NSP")
  ) +
  theme_minimal() +
  theme(
    plot.title = element_text(face = "bold"),        # Mettre le titre en gras
    axis.title.x = element_text(hjust = 1),          # Aligner le titre de l'axe x à droite
    axis.title.y = element_text(hjust = 1),          # Aligner le titre de l'axe y à droite
    axis.text.x = element_text(angle = 45, hjust = 1), # Incliner les étiquettes de l'axe x à 45°
    plot.caption = element_text(hjust = 0, size = 8)   # Aligner la source à gauche et réduire la taille de police
  ) +
  facet_grid(PCS ~ Sexe)  # Une facette pour chaque combinaison

2.3.2.3 Exporter et intégrer un graphique ggplot2 dans un document

Il existe deux méthodes principales pour exporter un graphique créé avec ggplot2 :

• Via la fenêtre Plots de l’interface RStudio
  Vous pouvez simplement cliquer sur le menu Export dans la fenêtre graphique, puis choisir le format et la taille de l’export.
  

Export via l’interface RStudio

• Via la fonction ggsave()  Cette fonction permet de sauvegarder les graphiques dans divers formats raster (.png, .pdf, .jpeg) ou vectoriels (.svg). Le format .svg est particulièrement adapté pour les graphiques ou images qui doivent être redimensionnés sans perdre en qualité, ou lorsque l’on souhaite retoucher la figure obtenue à l’aide d’un logiciel de traitement d’images. Cela le rend idéal pour les publications où une résolution élevée est nécessaire, car il conserve sa netteté, quel que soit le zoom ou la taille de l’image, et peut être facilement adapté par les services éditoriaux pour le mettre en conformité avec leur charte graphique. 

Arguments de ggsave() 

La fonction ggsave() comprend plusieurs arguments:

• filename : Nom du fichier de sortie (si le chemin du fichier de sortie n’est pas précisé, ggsave sauvegarde par défaut le graphique dans le répertoire de travail par défaut de l’utilisateur).
• plot : L’objet graphique à sauvegarder (par défaut, ggsave() utilise le dernier graphique généré).
• width et height : Les dimensions du graphique en pouces (inch). L’ajustement de ces dimensions peut souvent nécessiter un peu de tâtonnement en fonction de l’usage prévu.
• dpi : La résolution pour les formats raster (par exemple, 300 dpi pour une impression de haute qualité). 

Le code permettant de sauvegarder les graphiques fournissant pour chaque sexe (Homme puis Femme) la distribution des opinions selon la PCS en format .png avec la fonction ggsave() figure ci-dessous:

Sexe_Opinion_PCS_Graph <- ggplot(Sexe_Opinion_PCS, aes(x = PCS, y = Freq, fill = Opinion)) +
  geom_bar(stat = "identity") +
  labs(
    title = "Distribution (en %) des opinions des enquêtés sur la\nprise en charge des personnes âgées à domicile,\nen fonction de la PCS",
    x = "PCS",
    y = "Pourcentage",
    fill = "Opinion",
    caption = "Source : ERFI 1, vague 1, 2005, INED/INSEE"
  ) +
  scale_fill_viridis_d(
    name = "Responsabilité\nprise en charge\ndes personnes âgées\nà domicile",
    labels = c("La société", "Plutôt la société", "Les deux", "Plutôt la famille", "La famille", "NSP")
  ) +
  theme_minimal() +
  theme(
    plot.title = element_text(face = "bold"),        # Mettre le titre en gras
    axis.title.x = element_text(hjust = 1),          # Aligner le titre de l'axe x à droite
    axis.title.y = element_text(hjust = 1),          # Aligner le titre de l'axe y à droite
    axis.text.x = element_text(angle = 45, hjust = 1), # Incliner les étiquettes de l'axe x à 45°
    plot.caption = element_text(hjust = 0, size = 8)  # Aligner la source à gauche et réduire la taille de police
  ) +
  facet_wrap(~ Sexe)  # Une facette par sexe
 

ggsave("Sexe_Opinion_PCS.png", plot = Sexe_Opinion_PCS_Graph, width = 6, height = 4, dpi = 300) #Sauvegarde du graphique dans le répertoire de travail actuel

Définir le chemin de sauvegarde

Lorsque vous utilisez la fonction ggsave() pour exporter un graphique, vous devez spécifier le chemin où le fichier sera sauvegardé. Le chemin peut être relatif ou absolu, selon vos besoins.
Plusieurs types de chemin peuvent être définis.

• Répertoire de travail actuel (getwd())
  Si vous ne spécifiez pas de chemin, le fichier sera sauvegardé par défaut dans le répertoire de travail, c’est-à-dire le dossier où vous exécutez votre code. Pour connaître ce répertoire, vous pouvez utiliser la fonction getwd(), qui renvoie le chemin du répertoire de travail actuel.

#Sauvegarde d'un fichier dans le répertoire de travail actuel
ggsave("graphique.png")

• Chemin relatif
  Vous pouvez également spécifier un chemin relatif en indiquant un sous-dossier par rapport au répertoire de travail. Par exemple, si vous travaillez dans un projet RStudio, pour sauvegarder le graphique dans un sous-dossier appelé “plot”, vous pouvez écrire :

#Sauvegarde d'un fichier dans le sous-dossier graphique de votre projet R
ggsave("plot/graphique.png")

Les chemins relatifs sont particulièrement utiles lorsque vous travaillez dans des projets partagés ou sur des serveurs, car ils rendent votre code plus “portable”.

• Chemin absolu
  Un chemin absolu spécifie le chemin complet à partir de la racine de votre système de fichiers. Cela permet de sauvegarder le fichier dans un dossier spécifique, quel que soit le répertoire de travail.

#Sauvagarde dans dans le dossier spécifié, indépendamment du répertoire courant.
ggsave("C:/Utilisateurs/Moi/Documents/graphique.png")

Cette partie a présenté les étapes essentielles pour créer et personnaliser des graphiques avec ggplot2, depuis la sélection des données jusqu’à l’exportation finale du résultat. Elle met en lumière l’importance d’une approche méthodique, en abordant la personnalisation des axes, des couleurs, des légendes et des thèmes, ainsi que l’utilisation des facettes pour comparer des sous-groupes. 

Pour une vue d’ensemble rapide et synthétique des fonctionnalités de ggplot2, vous pouvez vous référer à la ggplot2 Cheat Sheet, un outil pratique qui résume les principales commandes et options disponibles. 
Ces bases vous permettront d’appliquer efficacement ggplot2, notamment dans la prochaine section consacrée à la reproduction de figures tirées d’un article scientifique.

3. Mise en pratique : reproduire les figures de l’article “A quelle fréquence voit-on ses parents ?” d’Arnaud Régnier-Loilier

L’objectif de cet exercice d’application est de reproduire à l’identique (ou presque) les figures 1 et 3 de l’article “A quelle fréquence voit-on ses parents?” d’Arnaud Régnier-Loilier.

3.1 Réplication de la figure 1 : graphique sans facet

3.1.1 Comprendre les données représentées et identifier le type de graphique

Il s’agit de deux courbes, qui représentent la proportion de personnes qui voient leur père/leur mère au moins une fois par semaine, selon l’âge au moment du départ du foyer parental.
L’âge au départ du foyer parental (regroupé en classes) est représenté sur l’axe des abscisses, et la fréquence de visite aux parents sur l’axe des ordonnées. Ce sont deux variables qualitatives. L’âge est une variable quantitative, mais elle a été ici discrétisée (regroupée en classes). On la traite donc comme une variable catégorielle.

En se référant au dictionnaire des codes de l’enquête, on identifie les noms des variables dont on aura besoin pour reproduire le graphique :

• Fréquence de visite à la mère : (PA_FQAVM_rec) ;
  
• Fréquence de visite au père : (PB_FQAVP_rec) ;
  
• Âge au départ du foyer parental : (PF_AGEDEPFOY_rec) ;
  
• Âge (au moment de l’enquête) : (MA_AGEM_rec) ;
  
• Parents encore en vie : (PA_MEREBV_rec) et (PB_PEREBV_rec) ;
  
• Pondération : (poids12).

Les trois premières variables sont celles représentées sur le graphique. L’âge au moment de l’enquête et les deux variables indiquant si les parents sont en vie permettent de restreindre le champ. Quant à la pondération, elle est essentielle lorsque l’on travaille à partir de données d’enquête collectées auprès d’un échantillon représentatif de la population totale.

Avertissement

Les deux variables représentées sur ce graphique sont toutes deux qualitatives. Le graphique en courbes n’est donc pas le choix le plus adapté, celui-ci étant normalement réservé aux séries temporelles. Néanmoins, l’âge étant une donnée relative au temps, il n’est pas rare d’utiliser des courbes pour visualiser graphiquement l’évolution d’un phénomène selon l’âge.

La figure telle qu’elle est dans l’article de Population & Sociétés présente deux “problèmes” :

• C’est une variable catégorielle sur l’axe des abscisses, or pour un graphique en courbes, cela devrait être une variable quantitative ;
  
• L’amplitude des classes d’âge au départ du foyer parental est inégale : l’espace entre deux graduations de l’axe des abscisses devrait être proportionnel à la taille de chaque classe, or ce n’est pas le cas.

On peut corriger cela en représentant les centres de classe sur l’axe des abscisses : il s’agira alors d’une variable quantitative, et les points seront donc plus ou moins espacés selon l’amplitude de la classe.
Une autre solution serait de calculer la proportion de personnes voyant leur père/ mère au moins une fois par semaine pour chaque âge détaillé. Cependant le découpage en classes permet de “lisser” les courbes et d’éviter des fluctuations liées à de faibles effectifs pour certains âges.

3.1.2 Préparation des données

3.1.2.1 Importer les données et sélectionner la population d’étude

Commençons par importer les données et charger les packages nécessaires à l’analyse :

# Installation de ggthemes si ce n'est pas déjà fait
if (!requireNamespace("ggthemes", quietly = TRUE)) {
  install.packages("ggthemes")
}

#chargement des packages
library(readr) ; library(questionr) ; library(tidyverse); library(ggthemes)

#import des données
ERFI1_FPA <- read_csv("data/ERFI1_FPA.csv")

La population représentée sur le graphique (indiquée dans le champ en dessous du graphique) est celle des personnes âgées de 30 à 79 ans dont les deux parents sont encore en vie.
Nous allons donc créer une sous-table contenant uniquement ces individus, qui servira de base pour les analyses ultérieures.

erfi <- filter(ERFI1_FPA, between(MA_AGEM_rec, 30, 79) & PA_MEREBV_rec == 1 & PB_PEREBV_rec == 1)

Vérifions l’absence de valeurs manquantes pour les variables d’intérêt :

#âge au départ du foyer parental
table(erfi$PF_AGEDEPFOY_rec, useNA = "always")

   0    2    3    4    5    6    7    8    9   10   11   12   13   14   15   16 
   9    2    3    3    2    3    1    4    3    5    5    4    6   24   34   62 
  17   18   19   20   21   22   23   24   25   26   27   28   29   30 <NA> 
 105  369  320  377  260  243  216  160  122   84   51   43   32   79    0 

#fréquence de visite à la mère
table(erfi$PA_FQAVM_rec, useNA = "always")

   0    1    2    3    9 <NA> 
 151 1304 1151   22    3    0 

#fréquence de visite au père
table(erfi$PB_FQAVP_rec, useNA = "always")

   0    1    2    3    9 <NA> 
 251 1300 1055   24    1    0 

Il n’y a aucune valeur manquante parmi les trois variables à représenter dans le graphique.

3.1.2.2 Recoder les variables

Le dictionnaire des codes fournit des informations sur les modalités des variables d’intérêt (« Fréquence de visite au père/à la mère » et « Âge au départ du foyer parental »). Cependant, ces modalités diffèrent de celles utilisées dans le graphique. Il est donc nécessaire de procéder à un recodage préalable.

Pour la fréquence de visite aux parents (PA_FQAVM_rec et PB_FQAVP_rec)
Il est nécessaire de recoder ces variables en deux catégories : « oui » si la personne voit son père/sa mère au moins une fois par semaine, et « non » si elle les voit moins souvent.

Comment traiter les réponses « Ne sait pas » ? Généralement, ces réponses sont soit conservées dans une catégorie distincte, soit considérées comme des valeurs manquantes si elles sont très peu nombreuses.
Dans notre cas, nous pouvons supposer que les personnes ayant répondu ne pas savoir à quelle fréquence elles voient leurs parents les voient de manière très irrégulière, donc moins d’une fois par semaine. Il semble donc raisonnable de les inclure dans la modalité “Non”.

#recodage de la fréquence de visite à la mère
erfi$VISITE_MERE <- as.character(erfi$PA_FQAVM_rec)
erfi$VISITE_MERE[erfi$PA_FQAVM_rec == "0"] <- "Non"
erfi$VISITE_MERE[erfi$PA_FQAVM_rec == "1"] <- "Non"
erfi$VISITE_MERE[erfi$PA_FQAVM_rec == "2"] <- "Oui"
erfi$VISITE_MERE[erfi$PA_FQAVM_rec == "3"] <- "Oui"
erfi$VISITE_MERE[erfi$PA_FQAVM_rec == "9"] <- "Non"

#recodage de la fréquence de visite au père
erfi$VISITE_PERE <- as.character(erfi$PB_FQAVP_rec)
erfi$VISITE_PERE[erfi$PB_FQAVP_rec == "0"] <- "Non"
erfi$VISITE_PERE[erfi$PB_FQAVP_rec == "1"] <- "Non"
erfi$VISITE_PERE[erfi$PB_FQAVP_rec == "2"] <- "Oui"
erfi$VISITE_PERE[erfi$PB_FQAVP_rec == "3"] <- "Oui"
erfi$VISITE_PERE[erfi$PB_FQAVP_rec == "9"] <- "Non"

#création des classes d'âge
erfi$AGE_DEP <- cut(erfi$PF_AGEDEPFOY_rec,
  include.lowest = TRUE,
  right = FALSE,
  breaks = c(0, 20, 22, 24, 26, 30, 79)
)

Astuce

Le code pour le recodage peut être généré en mode “clic-bouton” grâce aux add-ins irec() et icut() du package questionr. Plus d’explications et un exemple sont donnés dans le kit pédagogique “Initiation au traitement de données d’enquête avec R - ERFI-1”

3.1.2.3 Calculer les pourcentages

Nous allons calculer les pourcentages à représenter dans le graphique à l’aide de tableaux croisés. Les valeurs issues de ces tableaux seront extraites dans un objet de type data.frame, que nous utiliserons ensuite avec les fonctions de visualisation du package ggplot2.

Réalisation des tableaux croisés
Nous avons besoin des proportions de personnes qui voient leur père/leur mère au moins une fois par semaine, selon leur âge au moment de leur départ du foyer parental. Nous allons donc croiser AGE_DEP et VISITE_PERE d’une part, puis AGE_DEP et VISITE_MERE d’autre part.
Dans cet exemple, la variable d’âge au départ du foyer parental (AGE_DEP) est placée sur les lignes du tableau croisé, ce qui nécessite de calculer des pourcentages en ligne.
Enfin, comme nous utilisons les données d’une enquête réalisée auprès d’un échantillon représentatif de la population, il ne faut pas oublier d’utiliser la variable de pondération (poids12).
La fonction wtd.table du package questionr permet de réaliser des tableaux croisés en tenant compte de celle-ci, avec l’argument weights.

#fréquence de visite au père selon l'âge au départ du foyer parental
T_PERE <- wtd.table(erfi$AGE_DEP, erfi$VISITE_PERE, weights = erfi$poids12) |>  #on calcule le tableau croisé des effectifs pondérés
  lprop() #on calcule les % en ligne
T_PERE #on affiche le tableau pour vérification

         Non   Oui   Total
[0,20)    67.6  32.4 100.0
[20,22)   59.4  40.6 100.0
[22,24)   58.3  41.7 100.0
[24,26)   53.7  46.3 100.0
[26,30)   44.6  55.4 100.0
[30,79]   39.1  60.9 100.0
Ensemble  59.7  40.3 100.0

#fréquence de visite à la mère selon l'âge au départ du foyer parental
T_MERE <- wtd.table(erfi$AGE_DEP, erfi$VISITE_MERE, weights = erfi$poids12) |> 
  lprop()
T_MERE

         Non   Oui   Total
[0,20)    64.9  35.1 100.0
[20,22)   55.3  44.7 100.0
[22,24)   53.7  46.3 100.0
[24,26)   49.0  51.0 100.0
[26,30)   42.3  57.7 100.0
[30,79]   39.5  60.5 100.0
Ensemble  56.3  43.7 100.0

3.1.2.4 Création du data frame pour la représentation graphique

Nous avons stocké les résultats des tableaux croisés dans deux objets T_PERE (pour les fréquences de visite au père) et T_MERE (pour les fréquences de visite à la mère). Quelle est la classe de ces objets ?

class(T_PERE)

[1] "proptab" "table"  

class(T_MERE)

[1] "proptab" "table"  

Ces deux objets sont de classe table. La première étape va donc être de les transformer en data frame (format compatible avec les fonctions de représentation graphique issues de ggplot2). La fonction as.data.frame permet d’effectuer cette transformation.

T_PERE <- as.data.frame(T_PERE)
T_MERE <- as.data.frame(T_MERE)

#on vérifie que la classe des objets T_PERE et T_MERE est bien data frame
class(T_PERE)

[1] "data.frame"

class(T_MERE)

[1] "data.frame"

Intéressons-nous maintenant au contenu de ces data frame : chacun comporte 21 observations et 3 variables.

Var1	Var2	Freq
[0,20)	Non	64.93069
[20,22)	Non	55.26404
[22,24)	Non	53.70741
[24,26)	Non	49.02933
[26,30)	Non	42.28285
[30,79]	Non	39.51147

• Var1 : les classes d’âge au départ du foyer parental ;
  
• Var2 : voir son père/sa mère au moins une fois par semaine (Oui/Non) ;
  
• Freq : les pourcentages correspondant à chaque intersection dans le tableau croisé.

Commençons par renommer les variables Var1 et Var2 afin de leur attribuer des noms plus explicites. Cela améliore la lisibilité des traitements et leur reproductibilité.

Avertissement

Il est important de renommer Var1 et Var2 de la même manière dans T_MERE et T_PERE en vue de la fusion de ces deux tables par la suite.

#pour la fréquence de visite à la mère
T_MERE <- T_MERE |>  rename(AGE_DEP = Var1, VISITE = Var2)

#pour la fréquence de visite au père
T_PERE <- T_PERE |>  rename(AGE_DEP = Var1, VISITE = Var2)

Avant de fusionner les deux tables, nous ajoutons dans chacune une variable PARENT indiquant le parent auquel se rapportent les fréquences de visite, afin de différencier ces informations dans la table fusionnée. A nouveau, il importe de bien lui donner le même nom dans T_MERE et T_PERE.

T_MERE$PARENT <- "Mère"
T_PERE$PARENT <- "Père"

Nous regroupons les deux tables à l’aide de la fonction bind_rows (package dplyr inclus dans le tidyverse).

DATA <- bind_rows(T_MERE, T_PERE)

Sur le graphique, nous ne souhaitons représenter que les proportions de personnes ayant répondu voir leur père/mère au moins une fois par semaine. Nous allons donc conserver uniquement la modalité “Oui” pour la variable VISITE.
Nous ne souhaitons pas non plus représenter les marges du tableau croisé (ligne/colonne “Ensemble”). Nous allons donc supprimer la modalité “Ensemble” de la variable AGE_DEP.

DATA <- DATA |>  
  filter(VISITE == "Oui" & AGE_DEP != "Ensemble")

La dernière étape de préparation des données consiste à transformer les classes d’âge au départ du foyer parental (variable catégorielle AGE_DEP) en variable quantitative en prenant le centre de chaque classe, afin de pouvoir représenter cette variable sur l’axe des abscisses du graphique en courbes.
Pour cela, nous allons procéder à un nouveau recodage.

## Recodage de DATA$AGE_DEP en DATA$AGE_DEP_rec
DATA$AGE_DEP_rec <- as.character(DATA$AGE_DEP)
DATA$AGE_DEP_rec[DATA$AGE_DEP == "[0,20)"] <- "18.5"
DATA$AGE_DEP_rec[DATA$AGE_DEP == "[20,22)"] <- "20.5"
DATA$AGE_DEP_rec[DATA$AGE_DEP == "[22,24)"] <- "22.5"
DATA$AGE_DEP_rec[DATA$AGE_DEP == "[24,26)"] <- "24.5"
DATA$AGE_DEP_rec[DATA$AGE_DEP == "[26,30)"] <- "27.5"
DATA$AGE_DEP_rec[DATA$AGE_DEP == "[30,79]"] <- "34"

Note

Pour les classes “Moins de 20 ans” et “30 ans ou plus”, qui n’ont pas de borne inférieure ou supérieure définie, il faut faire un choix arbitraire pour déterminer le centre de classe.

• Pour la classe “moins de 20 ans”, si l’on fait l’hypothèse que la majorité des individus quittent le foyer parental à leur majorité, les bornes de cette classe seraient [18 ; 20[, le centre de classe est donc 18,5.
  
• Pour la classe “30 ans ou plus”, la valeur maximale possible est 79 ans (limite de la tranche d’âge interrogée dans l’enquête). Cependant les valeurs ne sont pas équiréparties au sein de la classe. Le choix fait ici est de prendre comme centre de classe la valeur médiane pour les individus de cette classe, soit 34 ans.

Puis nous transformons la variable recodée au format numérique.

DATA$AGE_DEP_rec <- as.numeric(DATA$AGE_DEP_rec)

Les données sont désormais prêtes pour la représentation graphique.

3.1.2.5 Réplication du graphique

Mise en place de l’esthétique (aes)

• Variable à représenter en abscisse (argument x) : âge au départ du foyer parental (AGE_DEP_rec) ;
  
• Variable à représenter en ordonnées (argument y) : proportion de personnes qui voient au moins un fois par semaine leur père/leur mère (Freq) ;
  
• Variable qui détermine la couleur et le type de trait de la courbe (arguments color et linetype) : le sexe du parent (PARENT).

DATA |>  #on indique dans quel data frame se trouvent les données à représenter
  ggplot(aes(x = AGE_DEP_rec,
             y = Freq,
             color = PARENT, linetype  = PARENT))

Mise en place des géométries

Nous souhaitons représenter un graphique en courbes, la géométrie à utiliser est donc geom_line

DATA |>  #nous indiquons dans quel data frame se trouvent les données à représnter
  ggplot(aes(x = AGE_DEP_rec,
             y = Freq,
             color = PARENT, linetype  = PARENT)) + #nous mettons en place l'esthétique
  geom_line() 

Ajuster les limites et les graduations des axes

Nous souhaitons que l’axe des ordonnées affiche les valeurs de 25 à 65 %, avec un pas de 5 points de pourcentage; et que l’axe des abscisses affiche de 18 à 34 ans, avec un pas de 2 années.
Etant donné que les deux variables représentées sur les axes x et y sont des données quantitatives (âge, AGE_DEP_rec et proportions pondérées, Freq), nous utilisons les fonctions scale_x_continuous et scale_y_continuous pour ajuster ces axes.
L’argument break permet de définir le pas. breaks = seq(a,b,c) indique que l’on souhaite graduer l’axe entre les valeurs a et b, avec un pas de c. Ainsi, pour graduer l’axe x entre 18 et 34 avec un pas de 2, nous indiquons scale_x_continuous(breaks = seq(18,34,2).
Si les limites de l’axe ne correspondent pas à celles souhaitées (par exemple, pour l’axe y, qui s’étend par défaut de 30 à 60 alors que nous souhaitons afficher de 25 à 65), nous pouvons ajouter l’argument limits = c(a,b), ou a est la valeur minimale et b la valeur maximale que nous souhaitons voir affichées sur l’axe.

DATA |>  #on indique dans quel data frame se trouvent les données à représenter
  ggplot(aes(x = AGE_DEP_rec,
             y = Freq,
             color = PARENT, linetype  = PARENT)) + #on met en place l'esthétique
  geom_line() + #on met en place les géométries
  scale_x_continuous(breaks = seq(18,34,2)) + #graduations de l'axe x
  scale_y_continuous(breaks = seq(25,65,5), limits = c(25, 65)) #graduations de l'axe y

Il ne reste plus qu’à améliorer la mise en forme et ajouter des éléments d’habillage autour du graphique.

3.3.4 Ajout des éléments d’habillage (titre, champ, source)

Nous utilisons la fonction labspour ajouter ou modifier les éléments d’habillage :

• title : ajouter le titre ;
• x et y : changer les titres des axes ;
• caption : ajouter un texte en dessous de graphique, ici le champ et la source.

DATA |>  #nous indiquons dans quel data frame se trouvent les données à représnter
  ggplot(aes(x = AGE_DEP_rec,
             y = Freq,
             color = PARENT, linetype  = PARENT)) + #nous mettons en place l'esthétique
  geom_line()  + #nous mettons en place les géométries
  scale_x_continuous(breaks = seq(18,34,2)) + #graduations de l'axe x
  scale_y_continuous(breaks = seq(25,65,5), limits = c(25, 65)) + #graduations de l'axe y
  labs (x = "Age au départ (ans)", #titre de l'axe x
        y = "En %", #titre de l'axe y
        title = "Proportions (%) d'enfants voyant au moins une fois par semaine\nleur père ou leur mère selon l'âge au départ du foyer parental", #titre du graphique
        caption = "Champ : Hommes et femmes âgés de 30 à 79 ans, dont les deux parents sont encore en vie\nSource : Ined-Insee, ERFI-GGS1, 2005") #ajout du champ et de la source

Mise en forme du graphique (couleurs, thème)

Les couleurs

Les couleurs associées à chaque courbe sont déterminées par le paramètre color dans l’esthétique du graphique. Pour modifier les couleurs par défaut, il faut utiliser la fonction scale_color_manual.

 DATA |>  #on indique dans quel data.frame se trouvent les données à représnter
  ggplot( aes(x = AGE_DEP_rec,
             y = Freq,
             color = PARENT, linetype  = PARENT)) + #nous mettons en place l'esthétique
  geom_line(stat="identity")  + #mise en places des géométries
  scale_x_continuous(breaks = seq(18,34,2)) + #graduations de l'axe x
  scale_y_continuous(breaks = seq(25,65,5), limits = c(25, 65)) + #graduations de l'axe y
  labs (x = "Age au départ (ans)", #titre de l'axe x
        y = "En %", #titre de l'axe y
        title = "Proportions (%) d'enfants voyant au moins une fois par semaine\nleur père ou leur mère selon l'âge au départ du foyer parental", #titre du graphique
        caption = "Champ : Hommes et femmes âgés de 30 à 79 ans, dont les deux parents sont encore en vie\nSource : Ined-Insee, ERFI-GGS1, 2005") + #ajout du champ et de la source
  scale_color_manual(name = "Voit au moins\nune fois par semaine :", #titre de la légende
                     values = c("#005b96", "#666e78"), #choix des couleurs
                     labels = c("Sa mère", "Son père")) #labels à associer à chaque couleur dans la légende

Le type de trait (pointillés ou trait plein)

Le type de trait correspond au paramètre linetype spécifié dans l’esthétique du graphique. La fonction scale_linetype_manual permet d’en modifier les paramètres.

Note

Actuellement, les couleurs et les types de trait font l’objet de deux légendes différentes. Pour fusionner les deux, il suffit de donner le même titre et les mêmes entrées de légende pour scale_linetype_manual et scale_color_manual.

 DATA |>  #nous indiquons dans quel data.frame se trouvent les données à représnter
  ggplot(aes(x = AGE_DEP_rec,
             y = Freq,
             color = PARENT, linetype  = PARENT)) + #nous mettons en place l'esthétique
  geom_line()  + #mise en place des géométries
  scale_x_continuous(breaks = seq(18,34,2)) + #graduations de l'axe x
  scale_y_continuous(breaks = seq(25,65,5), limits = c(25, 65)) + #graduations de l'axe y
  labs (x = "Age au départ (ans)", #titre de l'axe x
        y = "En %", #titre de l'axe y
        title = "Proportions (%) d'enfants voyant au moins une fois par semaine\nleur père ou leur mère selon l'âge au départ du foyer parental", #titre du graphique
        caption = "Champ : Hommes et femmes âgés de 30 à 79 ans, dont les deux parents sont encore en vie\nSource : Ined-Insee, ERFI-GGS1, 2005") + #ajout du champ et de la source
  scale_color_manual(name = "Voit au moins\nune fois par semaine :", #titre de la légende
                     values = c("#005b96", "#666e78"), #choix des couleurs
                     labels = c("Sa mère", "Son père")) + #labels à associer à chaque couleur dans la légende
  scale_linetype_manual(name = "Voit au moins\nune fois par semaine :", #titre de la légende
                        values = c(2, 1), #choix des types de trait
                        labels = c("Sa mère", "Son père")) #labels à associer à chaque type de trait dans la légende

Le thème

ggplot propose un certain nombre de thèmes pré-définis que l’on peut appliquer à son graphique. Pour notre graphique, nous allons utiliser le thème “black and white” (theme_bw()).

 DATA |>  #on indique dans quel data.frame se trouvent les données à représenter
  ggplot(aes(x = AGE_DEP_rec,
             y = Freq,
             color = PARENT, linetype  = PARENT)) + #nous mettons en place l'esthétique
  geom_line()  +  #mise en place des géométries
  scale_x_continuous(breaks = seq(18,34,2)) + #graduations de l'axe x
  scale_y_continuous(breaks = seq(25,65,5), limits = c(25, 65)) + #graduations de l'axe y
  labs (x = "Age au départ (ans)", #titre de l'axe x
        y = "En %", #titre de l'axe y
        title = "Proportions (%) d'enfants voyant au moins une fois par semaine\nleur père ou leur mère selon l'âge au départ du foyer parental", #titre du graphique
        caption = "Champ : Hommes et femmes âgés de 30 à 79 ans, dont les deux parents sont encore en vie\nSource : Ined-Insee, ERFI-GGS1, 2005") + #ajout du champ et de la source
  scale_color_manual(name = "Voit au moins\nune fois par semaine :", #titre de la légende
                     values = c("#005b96", "#666e78"), #choix des couleurs
                     labels = c("Sa mère", "Son père")) + #labels à associer à chaque couleur dans la légende
  scale_linetype_manual(name = "Voit au moins\nune fois par semaine :", #titre de la légende
                        values = c(2, 1), #choix des types de trait
                        labels = c("Sa mère", "Son père"))  + #labels à associer à chaque type de trait dans la légende
  theme_bw()

Nous souhaitons personnaliser le thème utilisé en en modifiant quelques éléments à l’aide de la fonction theme :

• mettre le titre en gras : plot.title = element_text(face = "bold")
  
• aligner les titres des axes à droite : axis.title.x = element_text(hjust = 1). Idem pour l’axe y avec axis.title.y.
  
• aligner le champ et la source à gauche, et réduire la taille de police de cet élément : plot.caption = element_text(hjust = 0, size = 8).

DATA |> #on indique dans quel data frame se trouvent les données à représnter
  ggplot(aes(x = AGE_DEP_rec,
             y = Freq,
             color = PARENT, linetype  = PARENT)) + #nous mettons en place l'esthétique
  geom_line()  +  #mise en place des géométries
  scale_x_continuous(breaks = seq(18,34,2)) + #graduations de l'axe x
  scale_y_continuous(breaks = seq(25,65,5), limits = c(25, 65)) + #graduations de l'axe y
  labs (x = "Age au départ (ans)", #titre de l'axe x
        y = "En %", #titre de l'axe y
        title = "Proportions (%) d'enfants voyant au moins une fois par semaine\nleur père ou leur mère selon l'âge au départ du foyer parental", #titre du graphique
        caption = "Champ : Hommes et femmes âgés de 30 à 79 ans, dont les deux parents sont encore en vie\nSource : Ined-Insee, ERFI-GGS1, 2005") + #ajout du champ et de la source
  scale_color_manual(name = "Voit au moins\nune fois par semaine :", #titre de la légende
                     values = c("#005b96", "#666e78"), #choix des couleurs
                     labels = c("Sa mère", "Son père")) + #labels à associer à chaque couleur dans la légende
  scale_linetype_manual(name = "Voit au moins\nune fois par semaine :", #titre de la légende
                        values = c(2, 1), #choix des types de trait
                        labels = c("Sa mère", "Son père"))  + #labels à associer à chaque type de trait dans la légende
  theme_bw() +
  theme(plot.title = element_text(face = "bold"), #mettre le titre en gras
        axis.title.x = element_text(hjust = 1), #aligner le titre de l'axe x à droite
        axis.title.y = element_text(hjust = 1), #aligner le titre de l'axe y à droite
        plot.caption = element_text(hjust = 0, size = 8)) #aligner le champ et la source à gauche et réduire la taille de police

3.2 Réplication de la figure 3 : graphique avec facets

Pour mettre en pratique la production de graphiques avec facettes (pour comparer deux ou plusieurs groupes entre eux), nous allons répliquer la figure 3 de l’article “A quelle fréquence voit-on ses parents ?”

Il y a une erreur dans le champ : celui-ci porte sur les personnes de 18 à 59 ans dont les deux parents sont encore en vie.

3.2.1 Identifier le type de graphique et les variables à utiliser

Il s’agit d’un graphique en courbes, qui représente la proportion de personnes qui voient au moins une fois par semaine leur père/leur mère, selon l’âge au moment de l’enquête. Le graphique est décliné selon le sexe de EGO.

Quelles sont les variables à mobiliser ?

• Fréquence de visite aux parents : PA_FQAVM_rec et PB_FQAVP_rec ;
  
• Âge au moment de l’enquête : MA_AGEM_rec (regroupé en classes) ;
  
• Sexe de EGO : MA_SEXE ;
  
• Parents encore en vie : PA_MEREBV_rec et PA_PEREBV_rec ;
  
• Pondération : poids12.

Nous procèderons à la même “correction” que précédemment pour l’axe des abscisses en prenant le centre de chaque classe d’âge.

3.2.2 Préparer les données

3.2.2.1 Filtrer le champ et vérifier l’absence de valeurs manquantes

Nous commençons par filtrer uniquement la sous-population concernée par le graphique : les 18-59 ans dont les deux parents sont encore en vie.

erfi_fig3 <- filter(ERFI1_FPA, between(MA_AGEM_rec, 18,59) & PA_MEREBV_rec == 1 & PB_PEREBV_rec == 1)

Nous vérifions l’absence de valeurs manquantes sur les variables à représenter

table(erfi_fig3$MA_AGEM_rec, useNA = "always")

  18   19   20   21   22   23   24   25   26   27   28   29   30   31   32   33 
  26   46   79   80   96  100  100  124  110  110  100  131  129  133  132  147 
  34   35   36   37   38   39   40   41   42   43   44   45   46   47   48   49 
 148  148  143  146  130  133  124  113   95   87   93   72   81   67   72   57 
  50   51   52   53   54   55   56   57   58   59 <NA> 
  47   51   43   40   30   26   35   27   29   14    0 

table(erfi_fig3$PA_FQAVM_rec, useNA = "always")

   0    1    2    3    9 <NA> 
 192 1779 1689   31    3    0 

table(erfi_fig3$PB_FQAVP_rec, useNA = "always")

   0    1    2    3    9 <NA> 
 326 1828 1505   33    2    0 

table(erfi_fig3$MA_SEXE, useNA = "always")

   1    2 <NA> 
1556 2138    0 

Aucune des variables utilisées ne présente de valeurs manquantes.

3.2.2.2 Recodage et format des variables

Nous procèdons ensuite au recodage des variables. Les deux variables de fréquence de visite aux parents peuvent être recodées exactement comme dans la partie précédente.

#recodage de la fréquence de visite à la mère
erfi_fig3$VISITE_MERE <- as.character(erfi_fig3$PA_FQAVM_rec)
erfi_fig3$VISITE_MERE[erfi_fig3$PA_FQAVM_rec == "0"] <- "Non"
erfi_fig3$VISITE_MERE[erfi_fig3$PA_FQAVM_rec == "1"] <- "Non"
erfi_fig3$VISITE_MERE[erfi_fig3$PA_FQAVM_rec == "2"] <- "Oui"
erfi_fig3$VISITE_MERE[erfi_fig3$PA_FQAVM_rec == "3"] <- "Oui"
erfi_fig3$VISITE_MERE[erfi_fig3$PA_FQAVM_rec == "9"] <- "Non"

#recodage de la fréquence de visite au père
erfi_fig3$VISITE_PERE <- as.character(erfi_fig3$PB_FQAVP_rec)
erfi_fig3$VISITE_PERE[erfi_fig3$PB_FQAVP_rec == "0"] <- "Non"
erfi_fig3$VISITE_PERE[erfi_fig3$PB_FQAVP_rec == "1"] <- "Non"
erfi_fig3$VISITE_PERE[erfi_fig3$PB_FQAVP_rec == "2"] <- "Oui"
erfi_fig3$VISITE_PERE[erfi_fig3$PB_FQAVP_rec == "3"] <- "Oui"
erfi_fig3$VISITE_PERE[erfi_fig3$PB_FQAVP_rec == "9"] <- "Non"

Quant aux classes d’âge, leur recodage s’apparente à celui des classes d’âge au départ du foyer parental réalisé plus haut. Là encore, nous pouvons générer le code nécessaire au découpage en classes grâce à l’add-in icut() du package questionr.
En ajoutant l’argument labels au code généré, nous pouvons labelliser chaque classe par sa valeur centrale, au lieu du label [borne 1,borne 2) utilisé par défaut. Cela facilitera la conversion au format numérique pour la représentation graphique.

#création des classes d'âges
erfi_fig3$AGE_CL <- cut(erfi_fig3$MA_AGEM_rec,
  include.lowest = TRUE,
  right = FALSE,
  breaks = c(18, 20, 25, 30, 35, 40, 45, 50, 55, 59),
  labels = c(18.5, 22, 27, 32, 37, 42, 47, 52, 57)
)

class(erfi_fig3$AGE_CL)

[1] "factor"

La nouvelle variable AGE_CL est de type facteur. Bien que ses labels soient des valeurs numériques, il est déconseillé de la convertir directement au format numérique car cela pourrait entraîner des résultats inattendus. Il est préférable de la convertir au préalable au format caractère, au format numérique.

erfi_fig3$AGE_CL <- as.character(erfi_fig3$AGE_CL) |> 
  as.numeric()

class(erfi_fig3$AGE_CL)

[1] "numeric"

summary(erfi_fig3$AGE_CL)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  18.50   27.00   37.00   35.51   42.00   57.00 

Enfin, la variable sexe (MA_SEXE), que nous allons utiliser pour définir les facettes du graphique, est de type numérique, codée “1” pour les hommes et “2” pour les femmes. Il est préférable de la convertir en facteur afin de s’assurer de l’ordre des modalités (les hommes à gauche puis les femmes à droite sur le graphique) et de lui associer des labels qui seront affichés sur les facettes du graphique.

class(erfi_fig3$MA_SEXE)

[1] "numeric"

erfi_fig3$MA_SEXE <- factor(erfi_fig3$MA_SEXE,
                            levels = c(1,2), #niveaux du facteur : modalités existantes, dans l'ordre dans lesquelles ont veut les voir apparaître
                            labels = c("Hommes", "Femmes")) #labels associés à chaque niveau du facteur

class(erfi_fig3$MA_SEXE)

[1] "factor"

levels(erfi_fig3$MA_SEXE)

[1] "Hommes" "Femmes"

3.2.2.3 Calcul des pourcentages

Il nous faut calculer les proportions pondérées d’hommes et de femmes qui voient leur père/leur mère selon la classe d’âges.
Pour simplifier le code, nous allons calculer les pourcentages en utilisant les verbes summarize et mutate du package dplyr (inclus dans le tidyverse).

Pour les visites au père :

data_pere <- erfi_fig3 |> 
  group_by(AGE_CL, MA_SEXE, VISITE_PERE) |> #nous groupons les individus selon leur classe d'âges, leur sexe et leur fréquence de visite à leur père
  summarize(n = sum(poids12),#nous faisons la somme des poids des individus appartenant à chaque groupe (numérateur de la proportion pondérée)
            .groups = "drop") |> #nous supprimons les groupes 
  group_by(AGE_CL, MA_SEXE) |> #nous groupons les individus selon leur classe d'âges et leur sexe
  mutate(freq = n/sum(n)) #calcul de la proportion pondérée : nous divisons n par la somme des n pour chaque groupe

head(data_pere)

# A tibble: 6 × 5
# Groups:   AGE_CL, MA_SEXE [3]
  AGE_CL MA_SEXE VISITE_PERE       n  freq
   <dbl> <fct>   <chr>         <dbl> <dbl>
1   18.5 Hommes  Non          26150. 0.351
2   18.5 Hommes  Oui          48286. 0.649
3   18.5 Femmes  Non          45418. 0.314
4   18.5 Femmes  Oui          99335. 0.686
5   22   Hommes  Non         412921. 0.503
6   22   Hommes  Oui         408470. 0.497

Pour les hommes âgés entre 18 et 19 ans (centre de classe 18,5), 65 % voient leur père au moins une fois par semaine et 35 % le voient moins souvent. La somme de ces deux proportions est bien égale à 100 %, confirmant que le calcul a été correctement réalisé.

Nous faisons de même pour les visites à la mère :

data_mere <- erfi_fig3 |> 
  group_by(AGE_CL, MA_SEXE, VISITE_MERE) |> #nous groupons les individus selon leur classe d'âges, leur sexe et leur fréquence de visite à leur mère
  summarize(n = sum(poids12),#nous faisons la somme des poids des individus appartenant à chaque groupe (numérateur de la proportion pondérée)
            .groups = "drop") |> #nous supprimons les groupes 
  group_by(AGE_CL, MA_SEXE) |> #nous groupons les individus selon leur classe d'âges et leur sexe
  mutate(freq = n/sum(n)) #calcul de la propotion pondérée : on divise n par la somme des n pour chaque groupe

head(data_mere)

# A tibble: 6 × 5
# Groups:   AGE_CL, MA_SEXE [3]
  AGE_CL MA_SEXE VISITE_MERE       n  freq
   <dbl> <fct>   <chr>         <dbl> <dbl>
1   18.5 Hommes  Non          17453. 0.234
2   18.5 Hommes  Oui          56983. 0.766
3   18.5 Femmes  Non          39293. 0.271
4   18.5 Femmes  Oui         105461. 0.729
5   22   Hommes  Non         381704. 0.465
6   22   Hommes  Oui         439687. 0.535

Nous regroupons les deux tables :

#Nous ajouronste une variable "parent" dans chaque table
data_pere$parent <- "Père"
data_mere$parent <- "Mère"

data <- bind_rows(data_pere, data_mere)

Note

Des valeurs manquantes NA sont apparues pour les variables VISITE_MERE et VISITE_PERE car celles-ci ne sont pas présentes dans les deux tables (VISITE_PERE n’est pas présente dans data_mere et inversement). Ce n’est pas un problème car ces variables ne sont pas directement représentées sur le graphique. Ce sont les proportions pondérées calculées à partir de ces variables qui le sont (variable freq), et il n’y a pas de valeurs manquantes pour celle-ci.

Dans le graphique, nous souhaitons représenter uniquement les proportions de personnes qui voient leur mère ou leur père au moins une fois par semaine, donc on ne va conserver que les lignes “Oui” pour VISITE_PERE ou VISITE_MERE.

data <- filter(data, VISITE_MERE == "Oui" | VISITE_PERE == "Oui")

is.data.frame(data) #on vérifie que data est bien de type data frame

[1] TRUE

Les données sont désormais prêtes pour la représentation graphique.

3.2.3 Réalisation du graphique

Mise en place de l’esthétique

• Axe des abscisses (x) : classes d’âge (variable AGE_CL) ;
• Axe des ordonnées (y) : proportions pondérées (variable freq) ;
  
• Couleur (color) et type de trait (linetype) : définis par le sexe du parent (variable parent).

data |>  
  ggplot(aes(x = AGE_CL, y = freq*100, color = parent, linetype = parent))

#nous multiplions freq par 100 pour afficher les valeurs en pourcentage (p. ex. 40 % au lieu de 0.4)

Nous ajoutons les géométries. Nous souhaitons représenter des courbes, il faut donc utiliser geom_line.

data |> 
  ggplot(aes(x = AGE_CL, y = freq*100, color = parent, linetype = parent)) +
  geom_line()

Note

Les courbes obtenues ont pour l’instant une forme étrange car il y a deux valeurs pour chaque classe d’âges et chaque parent : une pour les hommes et une pour les femmes. Comme nous n’avons pas encore spécifié les facettes (étape suivante), ggplot représente ces deux points sur la même courbe, ce qui explique par exemple la barre verticale sur la courbe relative aux visites à la mère à 32 ans.

Mise en place des facettes avec la fonction facet_wrap. On utilise la variable MA_SEXE pour spécifier les différentes facettes.

data |>  
  ggplot(aes(x = AGE_CL, y = freq*100, color = parent, linetype = parent)) +
  geom_line() +
  facet_wrap(~MA_SEXE) #mise en place des facettes

Nous ajustons les limites et les graduations des axes avec les fonctions scale_x_continuous et scale_y_continuous.

• Pour l’axe x : de 20 à 60 avec un pas de 10 ;
  
• Pour l’axe y : de 30 à 80 avec un pas de 10.

data |> 
  ggplot(aes(x = AGE_CL, y = freq*100, color = parent, linetype = parent)) +
  geom_line() +
  facet_wrap(~MA_SEXE) + #mise en place des facettes
  scale_x_continuous(breaks = seq(20,60,10)) + #graduations axe x
  scale_y_continuous(breaks = seq(30,80,10), limits = c(30,80)) #graduations et limites axe y

Nous ajoutons les éléments d’habillage avec la fonction labs.

data |>  
  ggplot(aes(x = AGE_CL, y = freq*100, color = parent, linetype = parent)) +
  geom_line() +
  facet_wrap(~MA_SEXE) + #mise en place des facettes
  scale_x_continuous(breaks = seq(20,60,10)) + #graduations axe x
  scale_y_continuous(breaks = seq(30,80,10), limits = c(30,80)) + #graduations et limites axe y
  labs(title = "Proportion (%) d'enfants voyant au moins une fois par semaine\nleur père ou leur mère selon l'âge",
       x = "Âge (ans)", y = "En %",
       caption = "Champ : femmes et hommes âgés de 18 à 59 ans dont les deux parents sont encore en vie\nSource : Ined-Insee, ERFI-GGS1, 2005")

Choix des couleurs et des types de traits

data |>  
  ggplot(aes(x = AGE_CL, y = freq*100, color = parent, linetype = parent)) +
  geom_line() +
  facet_wrap(~MA_SEXE) + #mise en place des facettes
  scale_x_continuous(breaks = seq(20,60,10)) + #graduations axe x
  scale_y_continuous(breaks = seq(30,80,10), limits = c(30,80)) + #graduations et limites axe y
  labs(title = "Proportion (%) d'enfants voyant au moins une fois par semaine\nleur père ou leur mère selon l'âge",
       x = "Âge (ans)", y = "En %",
       caption = "Champ : femmes et hommes âgés de 18 à 59 ans dont les deux parents sont encore en vie\nSource : Ined-Insee, ERFI-GGS1, 2005") +
  scale_color_manual(name = "Voit au moins\nune fois par semaine :",
                     values = c("#005b96", "#666e78"),
                     labels = c("Sa mère", "Son père")) + #changement des couleurs
  scale_linetype_manual(name = "Voit au moins\nune fois par semaine :", 
                        values = c(2, 1), 
                        labels = c("Sa mère", "Son père")) #changement des types de traits

Ajout et personnalisation du thème

data |>  
  ggplot(aes(x = AGE_CL, y = freq*100, color = parent, linetype = parent)) +
  geom_line() +
  facet_wrap(~MA_SEXE) + #mise en place des facettes
  scale_x_continuous(breaks = seq(20,60,10)) + #graduations axe x
  scale_y_continuous(breaks = seq(30,80,10), limits = c(30,80)) + #graduations et limites axe y
  labs(title = "Proportion (%) d'enfants voyant au moins une fois par semaine\nleur père ou leur mère selon l'âge",
       x = "Âge (ans)", y = "En %",
       caption = "Champ : femmes et hommes âgés de 18 à 59 ans dont les deux parents sont encore en vie\nSource : Ined-Insee, ERFI-GGS1, 2005") +
  scale_color_manual(name = "Voit au moins\nune fois par semaine :",
                     values = c("#005b96", "#666e78"),
                     labels = c("Sa mère", "Son père")) + #changement des couleurs
  scale_linetype_manual(name = "Voit au moins\nune fois par semaine :", 
                        values = c(2, 1), 
                        labels = c("Sa mère", "Son père")) + #changement des types de traits
  theme_bw() +
  theme(plot.title = element_text(hjust = 0.5, face = "bold"),#titre centré et en gras
        legend.position = "bottom", #placer la légende en bas
        plot.caption = element_text(hjust = 0, size = 8)) #aligner le champ et la source à gauche et réduire la taille de police

Cette formation ne présente qu’une petite partie des possibilités de représentations graphiques offertes par ggplot2. Néanmoins, vous possédez désormais les bases nécessaires pour poursuivre l’exploration de ce package en toute autonomie et créer vos propres représentations graphiques à partir de vos données !

Histogramme (geom_histogram()) Boxplot (geom_boxplot()) Densité (geom_density()) Diagramme en barre (geom_bar()) Nuage de points (geom_point()) Ligne (geom_line()) Export via l’interface RStudio

Notes de bas de page

1. La science ouverte est « la diffusion sans entrave des résultats, des méthodes et des produits de la recherche scientifique» (Deuxième Plan National pour la Science Ouverte, 2021)

2. Lorsqu’un graphique est créé à partir d’un data frame contenant des valeurs manquantes, ggplot2 ne les représentera pas et peut renvoyer des résultats inattendus.